In the Name of the Father: Inheritance Systems and the Dynamics of State Capacity
This paper examines how the degree of gender-egalitarianism embedded in inheritance rules impacts state capacity at its early stages during medieval times. We present a theoretical model in which building state capacity enables nobles to raise taxes and overcome rivals. The model addresses the use of inheritance to consolidate landholding dynasties, also accommodating inter-state marriages between landed heirs. On the one hand, dynastic continuity —of utmost importance to European medieval lords— directly encourages statebuilding. Male-biased inheritance rules historically maximise the likelihood of dynastic continuity. We weigh this effect against the indirect impact of the more frequent land merging marriages under gender-egalitarian rules. Contrary to the literature, our results suggest that gender-egalitarian norms —offering a low probability of dynastic continuity— promote state capacity in the short run more than gender-biased norms.
State capacity, Inheritance, Primogeniture, Marriage, Gender equality
Acknowledgements
I thank the participants of the “2015 Warwick Growth Economic Workshop” and the “8th Louvain Symposium in Economic Dynamics” an seminars at Brown University, Université catholique de Louvain and Université de Luxembourg for their useful comments. I am indebted to Jacob Weisdorf, David de la Croix, Luca Pensieroso and Fabio Mariani for their support, critiques and encouragement. Helpful suggestions and discussion with Thierry Verdier, Mathias Thoenig, Marc Goñi, David Weil and Mark Putterman have improved this paper. I thank the two anonymous referees for their comments on this paper. This research project was supported by an FSR grant on “Family, marriage and economic development” and the “ARC project 15/19-063” on “Family transformations: incentives and norms”, both financed by the French-speaking community of Belgium. This work was also supported by French National Research Agency Grant ANR-17-EURE-0020.
1 Introduction
Well-functioning states are the result of centuries of continuous improvements in state capacity. The economic literature documents a clear relationship between state capacity and economic development, with the former providing property rights, judicial systems and market-supporting institutions: Bockstette, Chanda, and Putterman (2002), Besley (2011), Fukuyama (2012). In particular, longer histories of state-level institutions are linked to economic prosperity in Chanda and Putterman (2007), Dincecco and Katz (2014) and Borcan, Olsson, and Putterman (2017).
Our theoretical paper is concerned with the process of building state capacity in its early stages, focusing on the resurgence of state centralisation in the European context during medieval times. The nascent states then replacing the Roman Empire invested in state capacity to provide security and defence against neighbours. In the economic literature, state capacity is usually expanded to overcome rivals and control resources. We examine this initial process of state-building, focusing on a neglected institutional factor: the degree of gender-egalitarianism embedded in inheritance rules. In doing so, we illustrate how gender equality may have impacted the process of state creation and, indirectly, affected economic prosperity, complementing the literature on state formation. However, this paper does not attempt to rationalise how modern states build state capacity. Specifically, we analyse how state capacity evolves under two different norms in the context of medieval Europe. We compare male-preference cognatic primogeniture, a norm that grants men preferential access to inheritance, with absolute primogeniture, a norm that treats genders alike. The choice of a particular rule is likely to be endogenous and possibly related to how women are perceived in a society. However, this paper exogenously fixes norms to compare their outcomes. Under the male-preference rule, a woman can only inherit if she has no living brothers. In contrast, absolute primogeniture selects the oldest sibling as heir, regardless of gender.
We introduce the concept of dynastic continuity, where landholdings are related to a family name for generations. A long-lasting system of identification was actively sought by European elites during the middle ages, as we detail later. As fiefs descend through inheritance, a member of the elite who expects his dynasty to continue will devote more resources to state capacity because its benefits remain attached to his family name. Male-biased inheritance rules incentivise state-building: historically, men ensured highly-valued dynastic continuity.1 In addition to this, our model accommodates inter-state marriages between land-inheriting heirs. These marriages lead to the accumulation of land, generating a wealth effect. We weigh the direct effect of more likely dynastic continuity under gender-biased norms against the wealth effect, more salient under gender-neutral rules.
Our model thus captures the incentive to build state capacity for land-based countries, as rulers sought territorial expansion to increase the prestige and influence of their dynasties. Although small and well-organised states did not territorially expand until late, their lords engaged in internal battles for control. Considering marriages intended to merge wealth and political power as well broadens the scope of our model and encompasses such cases, as Section 8 illustrates.
We find that state capacity accumulates faster under gender-egalitarian rules in the short run. This novel result revises the literature and indicates that fast wealth accumulation can make up for lower probability of dynastic continuity. Nonetheless, in the long run results are reversed. The differing rate of inter-state marriages between inheritance rules explains our results. In particular, wealth accumulation through marriages is delayed under gender-biased norms, as this system naturally generates less marriages. However, the total number of possible marriages is fixed, and eventually both systems converge towards the same distribution of wealth. After wealth differences vanish, the direct effect of a higher probability of dynastic continuity dominates, delivering the higher levels of state capacity typically found in the economic literature. Moreover, this last result provides a rationale —beyond short-term considerations regarding dynastic continuity— for the pervasive prevalence of male-preference cognatic primogeniture in the European context. Finally, although our model principally addresses the evolution of state capacity, we conclude that gender equality may have had major indirect consequences on economic development through state capacity building.2
3 The Model
Our model is based on an overlapping generations framework with discrete time. Consider a region \(\mathcal{L}\) divided into smaller sub-regions at period \(t=0.\) Each sub-region is a manor, indexed by \(i=1,2,\ldots,I_{t}\). The size of manors, denoted \(x_{t}^{i}>0\), is normalised such that \(\sum_{i \in \mathcal{L}_t} x_{t}^{i} = 1\). Each manor is ruled by a Lord who lives for two periods and makes decisions when adult. His preferences are given by: \[ \mathcal{U}_{t}^{i}=\ln\left(c_{t}^{i}\right)+\gamma\ln\left(x_{t+1}^{i}\right), \tag{1}\] where \(c_{t}^{i}>0\) represents consumption during adulthood and \(x_{t+1}^{i}\in\left(0,1\right)\) the size of the manor his heir will receive, after the war process but before marriages. Future manor size is discounted by \(\gamma\in\left(0,1\right)\), the probability of dynastic continuity. As we show later, inheritance rules determine its value. For the moment, with probability \(1-\gamma\) dynastic continuity ends and the incumbent Lord derives no utility as his dynasty disappears, losing all prestige and influence. In that sense, Lords care about the continuation of their dynasty and not about the perpetuation of genetic material. The utility formulation indicates this clearly, with no value attached to having surviving offspring.20 Lords are in fact powerless to avoid dynastic extinction and strictly follow inheritance rules.21 Similarly, a small manor after the war process, captured by \(x_{t+1}^{i}\), only provides limited benefits in terms of prestige. The entire manor and dynasty may even disappear if the Lord does not invest enough in state capacity and the army.22
Since total area is constant, the size of a manor can increase only at the expense of some neighbour. Conflict continuously arises because Lords seek to enlarge their estates. We model conflict through a war process such that, at every period of time, Lords battle all-against-all.23 Lords hire soldiers to battle and their efficiency is increased by state capacity. Following Skaperdas (1996), the outcome of the war is a new distribution of land: \[ x_{t+1}^{i}=\frac{\left(1+A_{t}^{i}+g_{t}^{i}\right)\left.b_{t}^{i}\right.^{\phi}}{\sum_{i\in\mathcal{L}_{t}}\left(1+A_{t}^{i}+g_{t}^{i}\right)\left.b_{t}^{i}\right.^{\phi}},\forall i\in\mathcal{L}_{t}, \tag{2}\] where \(b_{t}^{i}>0\) is the number of soldiers hired, \(\phi>0\) measures their relative importance in the war process, \(A_{t}^{i}\) represents state capacity during period \(t\) and \(g_{t}^{i}\) indicates the amount invested in state-building.24 We argue that a more capable state better organises its military because it has more officials and better internal coordination. To simplify the problem, we assume that Lords ignore the externality caused by a unilateral increase in the number of soldiers or in state capacity. This allows analytical results to be derived, at the expense of inconsistent behaviour when there is only one manor.25 However, the qualitative results —especially during the transition phase, when multiple manors exist— would not change if we adopted a more complex approach. Substituting Equation 2 into Equation Equation 1 yields an equivalent expression for utility: \[ \mathcal{U}_{t}^{i}=\ln\left(c_{t}^{i}\right)+\gamma\ln\left(\left(1+A_{t}^{i}+g_{t}^{i}\right)\left.b_{t}^{i}\right.^{\phi}\right),\forall i\in\mathcal{L}_{t}. \tag{3}\]
A Lord’s income depends on manor size and state capacity. In particular, a homogeneous final good is produced in each manor, using land alone.26 Total production is shared between the Lord and the commoners under a crop-sharing agreement.27 We impose constant shares over time and across manors: the Lord receives \(\psi\in\left(0,1\right)\) and the remaining \(1-\psi\) goes to the commoners. Further, the Lords can levy certain taxes on the commoners’ share. In keeping with the literature, the effective tax rate is given by \(\tau_{t}^{i}=\frac{A_{t}^{i}+g_{t}^{i}}{1+A_{t}^{i}+g_{t}^{i}}\) which increases in line with state capacity and investments. State capacity does not depreciate over time. Lord i’s budget constraint is: \[\begin{aligned} Z_{t}^{i} & \equiv & \psi Y_{t}^{i}+\left(1-\psi\right)Y_{t}^{i}\frac{A_{t}^{i}+g_{t}^{i}}{1+A_{t}^{i}+g_{t}^{i}}=c_{t}^{i}+p_{b}b_{t}^{i}+p_{g}g_{t}^{i}, \end{aligned} \tag{4}\] where \(p_{b}>0\) represents the costs associated with hiring a soldier and \(p_{g}>0\) the cost of increasing state capacity.28 Equation 1 and the budget constraint provide two reasons to invest in state capacity: first, it contributes positively to the outcome of war and, second, it allows for greater taxation. Given this, some Lords might invest in state capacity even when facing dynastic extinction, because tax income can be consumed.
Both the optimal number of soldiers, investment in state capacity and comparative statics are given in the following Propositions.
Proposition 1 The Lords’ optimal decision is given by the unique triplet \(\left(c_{t}^{i},b_{t}^{i},g_{t}^{i}\right)\) such that: \[\begin{aligned} \begin{split} b_{t}^{i}& =B\left(g_{t}^{i}\right)=% \frac{\gamma \phi (Y_{t}^{i} (\psi + A_{t}^{i}+g_{t}^{i} )-p_{b}g_{t}^{i} (1 + A_{t}^{i}+g_{t}^{i}))}{p_{b} (1+A_{t}^{i}+g_{t}^{i}) (1+\gamma \phi )}\\ g_{t}^{i}& =G\left(g_{t}^{i}\right)=\max\left\{ 0, g|G_{1}\left(g\right)=0\right\} , \\ c_{t}^{i}& =C\left(b_{t}^{i},g_{t}^{i}\right)=Z_{t}^{i}-p_{b}b_{t}^{i}-p_{g}g_{t}^{i}, \end{split} \end{aligned}\] where \(G_{1}\left(g_{t}^{i}\right)=% \frac{\gamma}{1+A_{t}^{i}+g_{t}^{i}}+% \frac{(1+\gamma \phi) \left(p_{g} (1+A_{t}^{i}+g_{t}^{i})^2-(1-\psi ) Y_{t}^{i}\right)}{(1+A_{t}^{i}+g_{t}^{i}) ( p_{g}g_{t}^{i} (1+A_{t}^{i}+g_{t}^{i})-Y_{t}^{i} (\psi+A_{t}^{i}+g_{t}^{i} ))}.\)
The next Propositions derive the main analytical results. First, Proposition 1 establishes the relationship between the probability of dynastic continuity, \(\gamma\), and state capacity building.
Proposition 2 State capacity building increases with the probability of dynastic continuity: \(\frac{\partial g_{t}^{i}}{\partial \gamma} \geq 0\).*
Corollary 1 Investments in state capacity are positive when dynastic continuity tends to zero if wealth \(Y_{t}^{i}\) is large enough, and accumulated state capacity \(A_{t}^{i}\) is low: \(\lim_{\gamma \to 0} g_{t}^{i} = \frac{Y_{t}^{i} \left( 1 - \psi \right)}{\sqrt{p_{g}}}-1-A_{t}^{i}\).*
Proposition 2 indicates that, as the probability of dynastic continuity increases, Lords optimally allocate more resources to increase state capacity. This relationship is akin to Proposition 6 in Besley and Persson (2009). Corollary 1 establishes that state-building is compatible with low likelihood of dynastic continuity. In that case, state capacity serves to increase tax revenue, which can be used for consumption. Other reasons may compel a Lord to invest in state capacity. For instance, investments can signal commitment to bureaucrats, reducing their incentive to revolt, particularly during transitions between Lords. Similarly, fertility is an endogenous variable that increases the probability of dynastic continuity under male-preference cognatic primogeniture, and Lords may be willing to trade off state capacity against higher values of \(\gamma\).29
We will weigh this effect against the indirect effect of more marriages under gender-egalitarian rules, which entail a lower probability of dynastic continuity. The effect of marriages operates through land-merging and affects manor sizes and wealth. Proposition 3 establishes that wealth positively affects state-building, a result familiar from the literature, see Proposition 4 in Besley and Persson (2009).
Proposition 3 State capacity building increases with wealth: \(\frac{\partial g_{t}^{i}}{\partial Y_{t}^{i}} \geq 0\).*
Finally, Proposition 4 presents additional comparative statics.
Proposition 4 At the optimum, \(\frac{\partial b_{t}^{i}}{\partial Y_{t}^{i}}>0\), \(\frac{\partial b_{t}^{i}}{A_{t}^{i}}>0\) and \(\frac{\partial g_{t}^{i}}{A_{t}^{i}}<0\). Also, at the optimum, \(\frac{\partial g_{t}^{i}}{\partial \psi}\geq 0\), \(\frac{\partial g_{t}^{i}}{\partial p_{b}}=0\), \(\frac{\partial g_{t}^{i}}{\partial p_{g}}<0\) and \(\frac{\partial g_{t}^{i}}{\partial \phi}<0.\) Regarding soldiers, we have that \(\frac{\partial b_t^{i}}{\partial \gamma}\geq 0\), \(\frac{\partial b_{t}^{i}}{\partial \phi}\geq 0\), \(\frac{\partial b_{t}^{i}}{\partial \psi}\geq 0\) and \(\frac{\partial b_{t}^{i}}{\partial p_{b}}<0\).*
Proposition 4 shows that army size increases in \(Y_{t}^{i}\) and \(A_{t}^{i}\). Moreover, \(g_{t}^{i}\) also increases with \(Y_{t}^{i}\). However, although \(g_{t}^{i}\) decreases with its accumulated level, if \(A_{t}^{j}>A_{t}^{i}\) then \(A_{t}^{j}+g_{t}^{j}>A_{t}^{i}+g_{t}^{i}\). Hence, a larger and more developed manor will capture more land from its opponents and, failing any counterbalancing force, it will continuously expand, creating an empire. Also, Proposition 4 indicates that the optimal number of soldiers decreases with its price. On the other hand, if the relative importance of soldiers in the war process, measured by \(\phi\), increases, the optimal response is to deploy more, thereby taking advantage of the value they add. Finally, a higher \(\psi\) means that Lords own more resources and depend less on taxation income, although it reduces the incentive to tax commoners. Since soldiers are a normal good, an increase in income increases demand for them. Similar reasoning can be applied to \(g_{t}^{i}\). The negative relationship with \(\phi\) follows from the substitutability between soldiers and state capacity.
A crucial aspect of this model is the delicate relationship between gender and surname-carrying. The surname-carrying gender —male— perpetuates the dynasty and institutions that favour male inheritance favour state capacity building, because Lords care about dynastic continuity. This generates the relationship between \(\gamma\) and state capacity in our model. In this respect, a gender-discriminating inheritance rule only promotes state capacity if heirship and surnames descend through the same gender. On the other hand, the number of men and women on the marriage market for land-inheriting heirs is balanced under a gender-neutral inheritance rule.30 Consequently, there are more marriages under this rule, and landholdings are merged more often and become larger.31 This provides an indirect lever that fosters state-building, as investments increase with Lords’ income.
3.1 Dynamics
Up to now we have restricted our attention to a static problem. This section describes the dynamic behaviour of the model, significantly influenced by the outcome of the marriage market and war, which consolidate landholdings. In what follows, we assume that tiny manors resulting from the war process are integrated into larger entities.32
In the context of the model, decisions are made under uncertainty with respect to dynastic continuity. In particular, an heir’s gender is only revealed at a testator’s death, and this announcement is deferred until the Lord’s offspring reaches adulthood.33 Taking this into consideration, we propose that events unfold in the following manner:34
Lords decide \(c_{t}^{i},\,b_{t}^{i}\,\mathrm{and}\,g_{t}^{i}\).
War takes place.
Heir’s gender is revealed and marriages are arranged.
3.2 Marriages
We consider a marriage market for land-inheriting heirs in which all participants have perfect information. Prospective spouses sort candidates according to wealth, that is, the preferred match is the richest individual of the opposite gender. As there are not necessarily the same number of men and women on this market, unmatched individuals are assumed to marry a non-heir child of a nobleman or a noble from elsewhere in the world. In medieval Europe, the elite deployed certain marriage strategies for their children: marriages were normally only arranged between spouses of similar rank.35 We capture this aspect by assuming that only potential spouses who are similar enough in terms of wealth can marry. In particular, the distance between them must be below a certain threshold, \(\delta_{t}\), for them to wed.36
Under these conditions, spouse selection follows a refined version of Gale and Shapley (1962). In our case, the outcome is intuitive. A Lord will marry his heir(ess) to the best possible candidate within his rank. This leads to a swift process of land concentration within the upper echelons of wealth distribution. Section 7 formalises the marriage market, and we assume that the state capacity of a merged manor is the average of its constituent parts.
It is important to note that inheritance rules and the stochastic realisation of children’s gender determine the outcome of the marriage market. In particular, heirs’ gender determines the number of men and women on the marriage market, and hence the number of possible marriages. Each inheritance rule incorporates mechanisms that can potentially lead to higher levels of state capacity. On the one hand, male-preference cognatic primogeniture offers a higher probability of dynastic continuity, directly encouraging state-building. Under such a rule a woman can only inherit if she has no living brothers. Therefore, a dynasty survives with a probability of \(1-0.5^\Phi\) for a man with \(\Phi\) children.37 This is higher than the respective probability under absolute primogeniture, 0.5, because the latter dictates that the oldest sibling inherits. Hence, discount rates are such that \(\gamma^{M}>\gamma^{A}\). On the other hand, absolute primogeniture balances the number of land-inheriting heirs and heiresses. Correspondingly, more land-merging occurs through marriages, which generates a wealth effect that encourages state-building. Because of the non-trivial, stochastic behaviour of the model when it comes to heirs’ gender, we resort to numerical simulations to analyse the implications of different inheritance rules.
4 Simulations and Results
At the beginning of each period, 30 manors exist. Simulations follow the steps outlined above, and we run 1000 simulations for each inheritance rule.
Parametrisation. The value of most of the parameters for the simulations is chosen from historical sources. The number of children per Lord comes from Russell (1958). French data show that 4.15 children survived their father. In England, the number was lower: 2.35. We take 3 as the number of children per Lord. Consequently, the effective discount rates are \(\gamma^{M}=1-0.5^{\Phi}=1-0.5^{3}\) and \(\gamma^{A}=0.5\).
The crop-sharing rule value is the average of the extreme cases presented in Slicher van Bath (1966). Therefore, \(\psi=5/12\). We use Sánchez Martı́nez et al. (2003) and Banegas López (2010) to compute the cost of soldiers, comparing their daily cost (2 sous) with the typical daily expenditure on food for a nobleman (1.6 sous). The real cost of a soldier is then \(p_{b}=1.2\).38 We proceed similarly to compute the cost of taxation. Following Verdés Pijuan (2004, 153), in the town of Cervera during the year 1424, the racional, that is, an auditor, received no less than 330 sous39 in yearly wages. A racional had to work three days a week or around 150 days per year, which gives us an equivalent wage of 2.2 sous per day. There is, though, a large discrepancy between this figure and English references.40 We initially follow the first estimate and set \(p_{g}=1.375\).
Finally, for each simulation we draw initial manor sizes \(\left(x_{t}^{i}\right)\) from a uniform distribution between 1 and 2 and we set the initial level of state capacity equal to zero. The disappearance threshold is set at \(\delta=0.01,\) that is, one-hundredth of the minimum original size. We use a time-varying marriage threshold equal to one standard deviation in manor size. The value of \(\phi\) is larger than 1 by assumption and equals \(1+\frac{1}{10^{11}}\), which delivers a slow evolution of the economy by hampering the effect war has on the distribution of manor sizes. Table 1 summarises the parametrisation.
| Parameter | Value | Source |
|---|---|---|
| \(\psi\) | 5/12 | Slicher van Bath (1966) |
| \(\Phi\) | 3 | Russell (1958). |
| \(\phi\) | \(1+1/10^{11}\) | Arbitrarily set to obtain slow transitions. |
| \(p_{b}\) | 1.375 | Banegas López (2010) and Sánchez Martı́nez et al. (2003). |
| \(p_{g}\) | 1.2 | Banegas López (2010) and Verdés Pijuan (2004). |
| \(\gamma^{M}\) | 7/8 | \(\gamma^{M}=1-0.5^\Phi.\) |
| \(\gamma^{A}\) | 1/2 | \(\gamma^{A}=1-0.5.\) |
| \(\delta\) | 0.01 | Arbitrarily set to 1/100 of the minimum initial size. |
In the remaining part of this Section, we comment on the results. Unless stated otherwise, marriages refer to marriages between a land-inheriting heir and heiress. Candidates on the marriage market are ranked according to the size of their manors.
Results: Figure 1 illustrates the evolution over time of the average level of state capacity for each inheritance rule. The solid line corresponds to male-preference cognatic primogeniture and the dashed line to absolute primogeniture.
Simulations provide evidence that, in the long run, a gender-biased inheritance rule allows higher average levels of state capacity to be achieved. However, it is also clear that, in the short run, gender-egalitarian rules boost state capacity more. This supports the previous intuition on the importance of marriages in merging manors and the significance of the income effect. In that sense, even if \(\gamma\) is lower under absolute primogeniture, wealth accumulation through marriages more than compensates for it.41 The subsequent reversal occurs because, in the long run, land is also concentrated through marriages under male-preference cognatic primogeniture, albeit at a slower rate. Thus, how long the rules apply is crucial in determining which of them is best, and the direct effect of dynastic continuity only dominates when the distribution of manor sizes is similar enough between regimes.
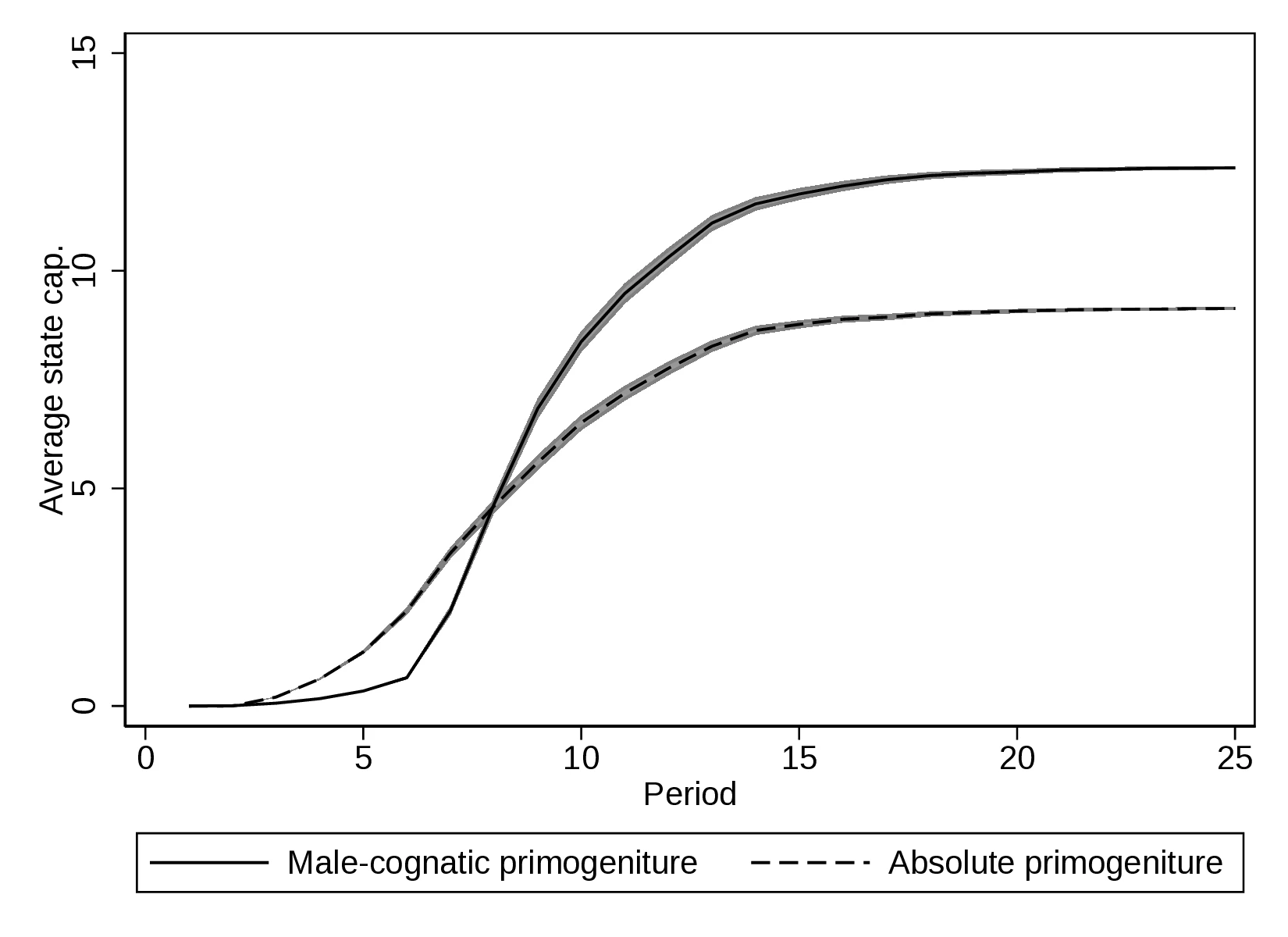
Notes: This Figure represents average levels of state capacity reached in the simulations for each period, distinguishing between inheritance rules. The solid line corresponds to male-preference cognatic primogeniture and the dashed line to absolute primogeniture.
As stated, marriages between heirs are a decisive factor in shaping the evolution of state capacity. When there are no restrictions on the marriage market, the marriage rate —that is, the total number of actual marriages relative to the number of participants in the market— is higher under absolute primogeniture.42 Our simulations show marriage rates of 0.41 and 0.125 for absolute and male-preference cognatic primogeniture respectively during the first period, when the number of participants is largest and \(\delta\) is less binding. Regional unification through marriage occurs faster initially under absolute primogeniture, generating larger manors that invest more in developing state capacity. This explains why this inheritance rule is associated with greater average state capacity in the short run.
On the other hand, a gender-biased rule promotes state capacity through the direct effect of \(\gamma\). Although initially, average manor size is smaller due to fewer marriages, the manors large enough to build state capacity are of similar size under both rules. Figure 2 (a) confirms this is the case, especially from period five onward. In these cases, \(\gamma^{M}>\gamma^{A}\) coupled with similar manor size results in higher average spending on state-building under male-preference cognatic primogeniture. Figure 2 (b) depicts average expenditure on building state capacity when only Lords investing a positive amount of resources are considered. Note that male-preference cognatic primogeniture overtakes absolute primogeniture even before manor size equalises, suggesting that the political stability conferred by dynastic continuity is a powerful driver of state-building. Finally, Figure 2 (c) presents the percentage of Lords that invest in state-building. Again, when manors are similar in size, not only do Lords invest more under male-preference cognatic primogeniture, but also more Lords invest.
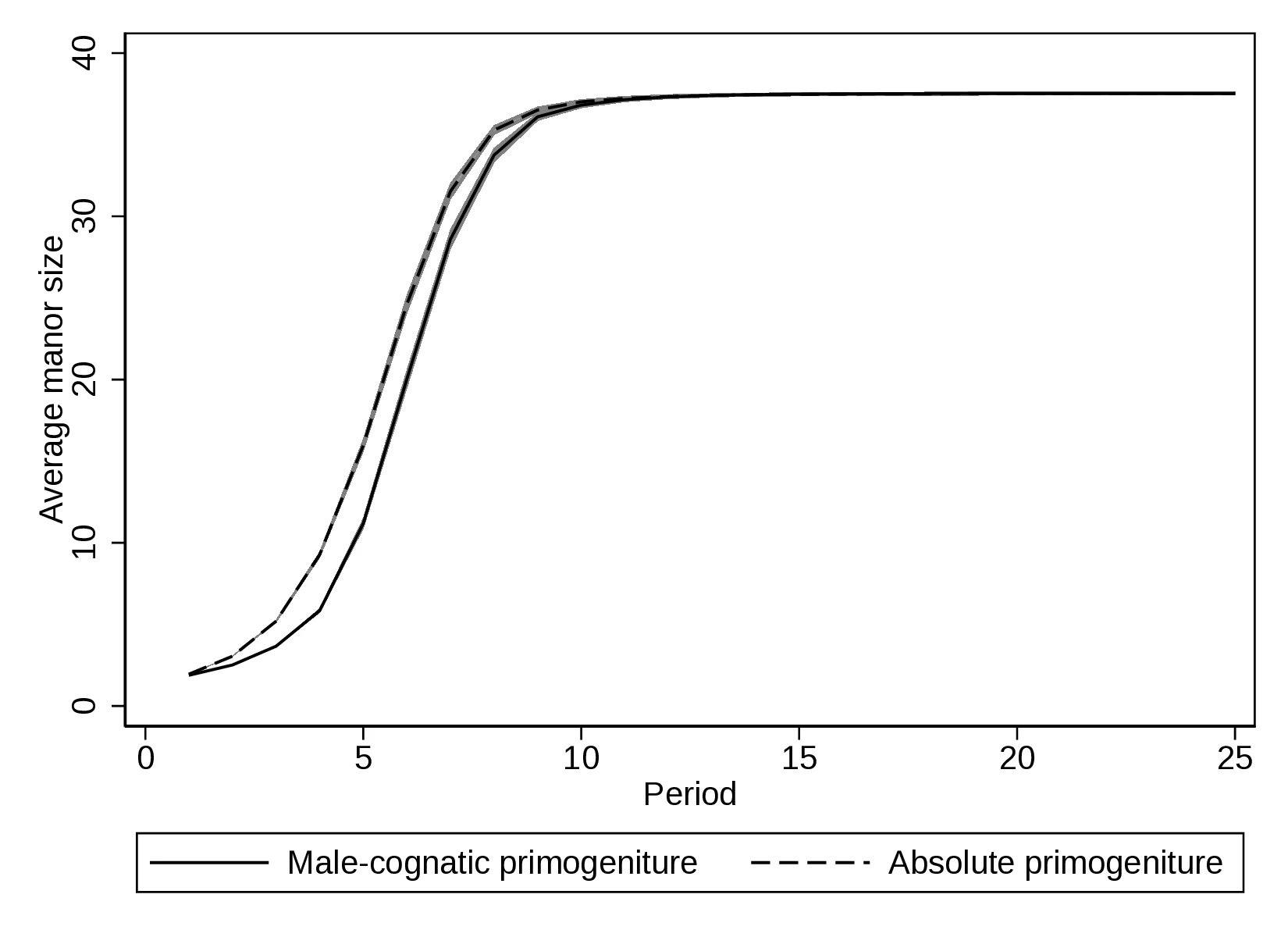
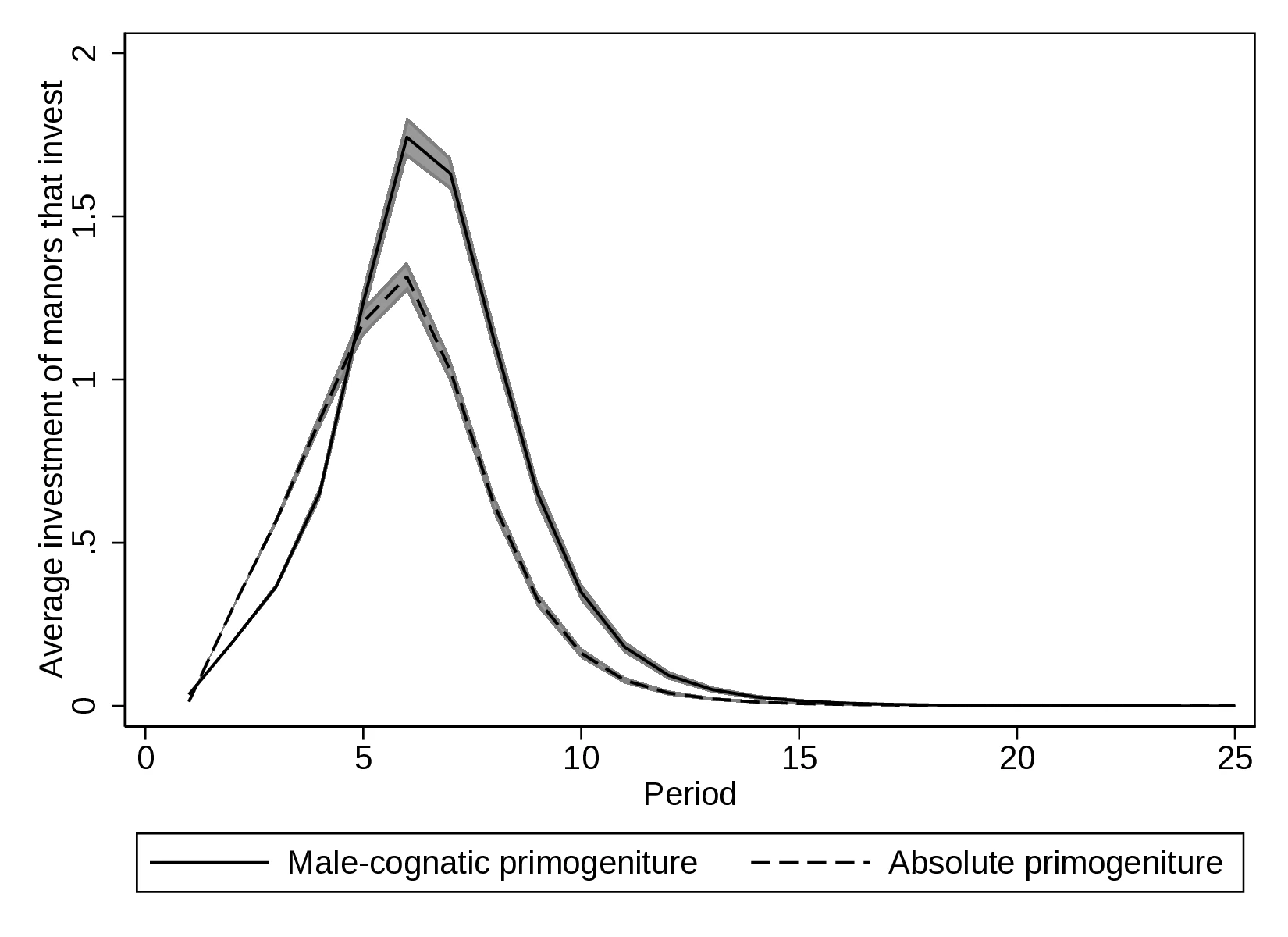

Notes: This Figure presents the average evolution of several variables. Figure 2 (a) depicts the average manor size of manors that build state capacity. Figure 2 (b) shows the average expenditure in state-building for the cases with positive investments. Finally, Figure 2 (c) presents the percentage of Lords that devote resources to state-building.
All in all, our simulations indicate that a higher probability of dynastic continuity does not guarantee higher levels of state capacity in the short run, once richer dynamics —inter-state marriages— are incorporated in the model. Nonetheless, in the long run, the importance of dynastic continuity re-emerges because income differences vanish with time. The number of marriages is limited and, eventually, a gender-discriminating rule catches up.43
Sensitivity analysis. Given the variations present in the estimates of the parameters, especially \(p_{g}\), we diligently conduct a series of robustness tests. In a first approach, we modify the value of the parameters one at a time. In all cases, the main result holds, that is, absolute primogeniture delivers higher levels of state capacity in the short run, only to be outperformed by male-preference cognatic primogeniture in the long run.
However, the dynamics are impacted, and the point at which male-preference cognatic primogeniture begins to outperform absolute primogeniture depends on the exact value of the parameters. We explore the relationship between the different parameters and this turning point in the relative performance of the two inheritance rules. In particular, starting from the baseline parametrisation in Table 1, we allow one parameter to take on different values while holding the rest at their baseline level. For each combination, we run one hundred simulations. Finally, we compute the average time at which male-preference cognatic primogeniture lastingly overtakes absolute primogeniture. Figure 3 presents the results. The horizontal axis represents the value of the parameter we change. The vertical axis indicates the average time at which male-preference cognatic primogeniture begins to deliver greater average state capacity. Notice that parameters vary over a relatively large interval.


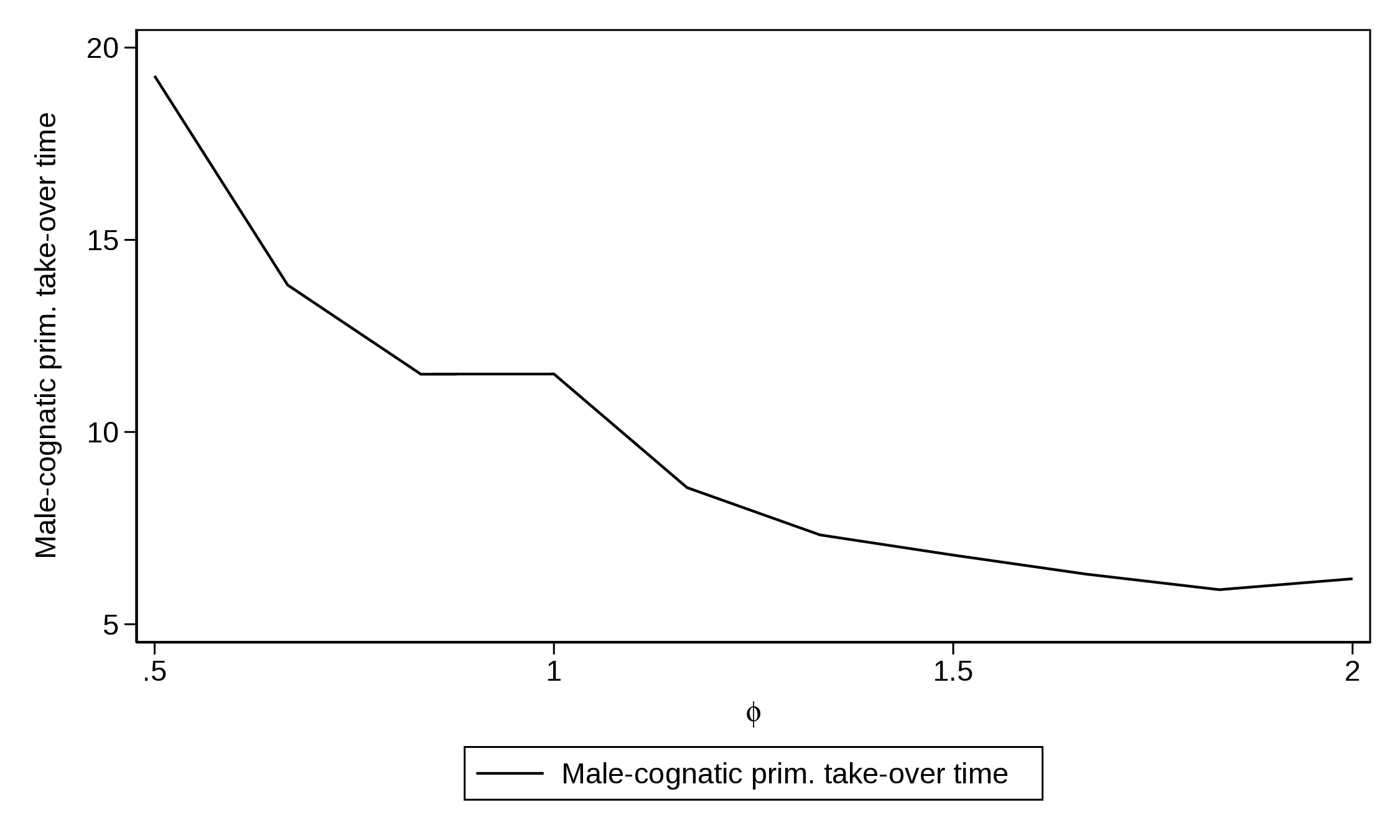

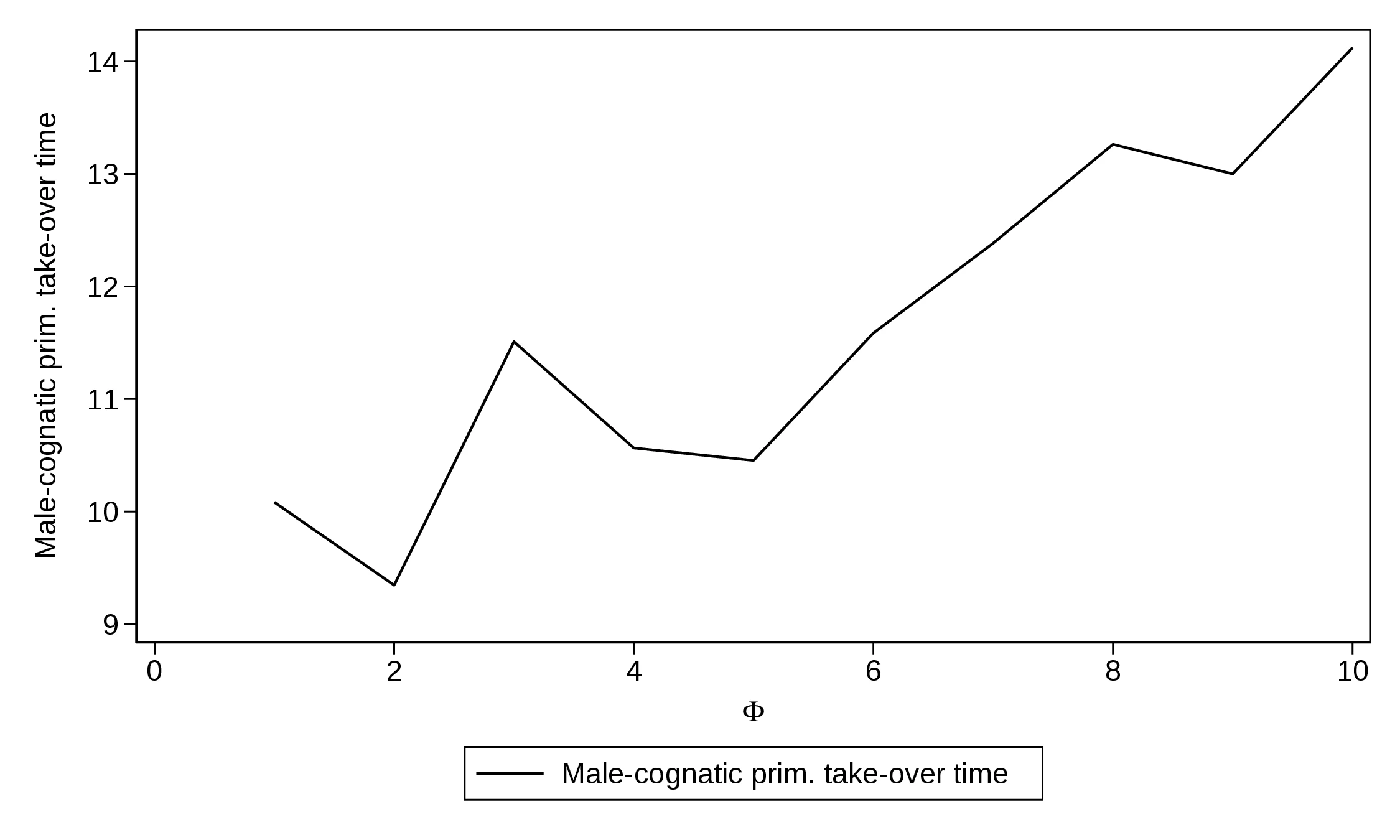
Notes: This Figure represents the time at which male-preference cognatic primogeniture overtakes absolute primogeniture in terms of average state capacity for different values of the parameters. Figure 3 (a) modifies the cost of building state capacity, \(p_g\). Figure 3 (b) changes the cost an army, \(p_b\) while Figure 3 (c) focuses on the effect soldiers have for the outcome of war, \(\phi\). Figure 3 (d) varies the share of output Lords appropriate, \(\psi\). Finally, Figure 3 (e) alters Lords’ offspring.
First, we focus on the effect of \(p_{g}\). Figure 3 (a) indicates that increasing \(p_{g}\) tends to slow down the process. In fact, the entire evolution of state capacity is delayed because investments are now more costly. However, the slowdown is more salient for male-preference cognatic primogeniture. This hints at the importance of the marriage market in generating manors that are wealthy enough to invest in state-building. Indeed, as \(p_{g}\) rises, the wealth threshold that determines investment in state capacity does so as well.
Second, values for \(p_{b}\) are changed and the rest held at their baseline level. Figure 3 (b) displays the results of this exercise. In general, no clear pattern emerges, and the spread of timing of male-preference cognatic primogeniture outperformance is tight. This is because the contribution of war toward wealth accumulation is similar under both norms. In particular, although Lords devote less resources to the army, the reduction is similar for all of them. Hence, the outcome of war is akin to that of the baseline case, as is the evolution of state capacity.
We continue by analysing the effect of \(\phi\), measuring men’s effect on war outcomes. The results are shown in Figure 3 (c). If \(\phi\) increases, deploying marginally more soldiers contributes more than linearly to the outcome of war —as long as \(\phi>1\)—. Hence, for a given difference in army size, higher values of \(\phi\) imply widening differences in the outcome. Therefore, as \(\phi\) grows, Lords that have vanquished neighbours appropriate more land from them. This speeds up wealth accumulation and, consequently, male-preference cognatic primogeniture reaches the threshold determining investment in state capacity faster.
The effect \(\psi\) has on the reversal of outperformance between absolute primogeniture and male-preference cognatic primogeniture is negative, as Figure 3 (d) reveals. The overall influence of \(\psi\) is twofold. On the one hand, a higher value means that Lords appropriate a larger share of output and rely less on taxation, which negatively impacts state-building. On the other hand, Lords are wealthier because they receive more output. The reversal clearly occurs later as \(\psi\) increases. Taken together, the reduced incentive to invest in state capacity dominates the wealth effect. In other words, the reduction in the marginal return on state capacity means that only wealthy Lords invest, and Lords are in general wealthier under absolute primogeniture.
Finally, we analyse the effect of changing Lords’ progeny, \(\Phi\), in Figure 3 (e). As noted previously, this has no effect under absolute primogeniture, as the heir is always the first-born and hence the discount rate \(\gamma^{A}\) remains constant at 0.5. However, \(\gamma^{M} = 1-0.5^{\Phi}\) and its exact value increases with Lords’ offspring, directly boosting state capacity. Nonetheless, a higher value of \(\Phi\) also reduces the probability that there will be an heiress under male-preference cognatic primogeniture —it equals \(0.5^\Phi\)—. As a consequence, the process of land accumulation through marriages is severely hindered. Simulations give mixed results. The direct effect is stronger at low levels of \(\Phi\), when \(\gamma^{M}\) rises more rapidly, as illustrated by the initial drop shown on the graph. However, despite a higher direct incentive, simulations indicate that the more offspring Lords have, the longer it takes male-preference cognatic primogeniture to outperform absolute primogeniture.
5 Conclusion
This paper addresses the evolution of state capacity at its early stages, focusing on the European medieval period. It shows that gender equality regarding access to inheritance affects the evolution of state capacity among nascent states during that time. Departing from the literature, it introduces inheritance rules and inter-state marriages in a simple theoretical model of state-building. The paper argues that the degree of gender-egalitarianism embedded in inheritance rules affects the development of state capacity. Two mechanisms are at play. First, the surname-carrying gender —typically male— ensures dynastic continuity. Institutions that favour male inheritance incentivise investments in state capacity because the nobility cares about dynastic continuity. Second, there is an indirect effect of more land-merging marriages under gender-egalitarian rules, which boosts income and encourages larger investments in state capacity. The role of dynastic continuity is often highlighted in the literature, but the second mechanism has been neglected. However, our analysis concerns only the historical evolution of state capacity and does not shed light on how modern states may build it.
Our results revise the importance of dynastic continuity, indicating that time considerations are relevant as well. In particular, gender-egalitarian rules —offering a lower probability of dynastic continuity— deliver higher levels of state capacity in the short run. However, this lead is only temporary: land-merging marriages take place under gender-discriminating rules, only the pace is slower. Since the number of possible marriages is finite, gender-biased rules catch up, landholdings become of similar size and the direct effect dominates. In addition to land, marriages can also merge wealth and political power, leading to a broader interpretation of the effects of inheritance rules, not confined to territorial-based states. Finally, in the light of the evidence relating state capacity and development, our results indicate that gender equality in inheritance rules indirectly affects the latter through the process of state-building.
The paper provides a rationale for the pervasive use of male-favouring inheritance rules in the European medieval context that goes beyond dynastic continuity: such rules also generate higher levels of state capacity. Despite the fact that European regions historically favoured men, precluding cross-country comparisons, our work still delivers some testable implications regarding state-building. First, the model indicates that regions where more marriages occurred were likely to develop state capacity more. Second, nobles who were fortunate enough to have a clear male, dynasty-continuing succession were likely to invest more resources in advancing the state. Finally, the importance of inter-state marriages was probably greater for small, high-capacity states not pursuing territorial expansion. These outcomes can be empirically tested.
6 Historical background
6.1 Feudalism and primogeniture
According to Reynolds (1996), under the feudal system first introduced by Carolingian rulers, lords were to “protect and maintain” vassals in exchange for military aid and court counselling in a society with no central government. This exchange involved transferring the control of fiefs from lords to vassals, to provide the latter with income to support their duties. Initially, this was only a lifetime arrangement, but its transmission through inheritance soon became common, and was already accepted for some domains as early as 877 in France and 1037 in Germany and Italy.
The military origins of fiefdom and the financial burden vassal obligations represented explain the prevalence of primogeniture, as “continual subdivision of and parcelling out of military tenures was a source of weakness to the organisation for the defence of the kingdom” (Cecil (1895, 31)). For such reasons, William I of England and Frederick Barbarossa declared honorary fiefs carrying duties indivisible, while King Edward I of England acknowledged that “undivided [lands] are quite sufficient for the service of the state [... but once] divided [...] no one portion suffices even for its owner’s maintenance”, see Willian Searle (1902, 3:174).
The importance of preserving estates complete is best exemplified by the practices employed. Noblemen generally had a large progeny to ensure dynastic continuity. However, some families forced up to 40% of their sons to remain single to avoid estate division, apparently jeopardising their direct genetic success, see Debris (2005, 24–26) and Hurwich (1998). Moreover, primogeniture ensured the economic success of only one son. Blocking the immediate transmission of genetic material or selecting a sole heir may seem counterproductive arrangements for the long-term diffusion of genetic material. However, Hrdy and Judge (1993) indicate these may be optimal in land-based societies.44 In particular, the authors argue that, if wealth determines marriage prospects, then bestowing land to a sole heir increases the probability of producing a grandson. In that sense, strategies that prevent estate division focus on the long-term survival of the dynasty: “unequal treatment of heirs was a strategy to minimize the probability of dying without surviving grandchildren”. Bergstrom (1994) reasons similarly and argues that keeping inheritances intact increased elite members’ fitness. Focusing on the aristocracy, Voland and Dunbar (1995) note that restraining fertility enhanced the heir’s fitness when the intertemporal preservation of status and lineage survival mattered. Chu (1991) offers a theoretical model focusing on this quality-quantity trade-off whereby primogeniture emerges as the optimal inheritance rule to avoid dynastic extinction.
Observers relate the cost of privately providing security to fief indivisibility. In fact, “the security of a landed estate depended upon its greatness”, whereas estate division would “ruin it” by easing “incursions of its neighbours”, see Smith (2015 [1776]). Blackstone (1766, 215) reasons similarly, adding that younger brothers were encouraged by the system to enter alternative occupations: the military, mercantile, civil and ecclesiastical positions, see also Betzig (1995) and Debris (2005, 24–25). The practice of fief indivisibility, particularly through primogeniture, better protected landownership against external attacks by selecting the eldest and most able son to inherit the responsibility of organising the defence, see Brenner (1985). However, external security came at the cost of internal instability caused by quarrels between siblings, see Bloch (1989, 134–35) and Duby (1983, 93–94).
Despite the general prevalence of primogeniture, estate division was a common practice during the early medieval times, and was gradually abandoned. Partition may have been an optimal system in earlier times, particularly if the cost of privately providing security and defence increased over time. In that sense, the shift in inheritance rules may reflect technological changes. Alternatively, agency problems in managing large estates could explain the adoption of inheritance division. In any case, ancient British custom dictated that all sons should share any inheritance, and in some regions women were also allowed to inherit (Cecil (1895, 26–27) and Patourel (1971)). The Saxons, however, represent a notable exception: typically, the eldest son was sole heir. William the Conqueror imported the Norman tradition of primogeniture, imposing it on military tenures. Other landholdings followed suit. Finally, around the 13th century in England, daughters shared an inheritance as co-heiresses if they had no living brothers, according to Brenner (1985). The author argues that dividing the inheritance avoided conflict between the husbands of the sisters. This was the case in the Marshal and Peverel families, see Leyser (2013, 119) and Ward (1995, 101). However, estate division was partly counteracted by sending younger daughters into monastic life, see Ward (1995, 21–22).
Transition from partitioning to intact inheritances occurred in French territories under the Capetian dynasty. Bloch (1961, 197) date the beginning of dynastic inheritance at around the year 1000 in Anjou and 1066 in Normandy, from where it reached the British Isles. Outside the common pattern, there were cases of divided inheritances: Evergates (2011) gives some examples in the province of Champagne between 1100 and 1300 and Barlow (1983) explains the process that culminated in the division of William the Conqueror’s possessions between his two eldest sons. Germanic tradition, however, varied over time. Inheritance was first established in 1037 by King Conrad II, who stated that land should descend to the son. The new ruling initially applied to Italian landholdings, but was subsequently introduced in Germany. It reached Carinthia, Swabia and Holland by the 12th century, unifying inheritance rules throughout the Empire. However, during the 13th century German princes embraced partitioning to exercise their power in opposition to the emperor. Primogeniture was restored as the inheritance rule after the Thirty Years War.
6.2 Women’s access to inheritance
A second aspect related to inheritance rules concerns the treatment of women. According to Herlihy (1962), barriers to female inheritance of land were first introduced by the Salic Law. This law completely banned women from inheriting land and brought about arguments and difficulties in identifying the proper heir. Barring women was aligned with the Germanic tribes’ customs, see Klapisch-Zuber et al. (1994, 171). King Chilperic relaxed the requirement and allowed women to inherit in the same way as men if all the surviving offspring were daughters. Other codes of law mutated as well, partly allowing women to inherit. For instance, Visigothic laws equally divided inheritances among all children in the case of intestate succession (Klapisch-Zuber et al. (1994, 177)). However, under several German codes, male preference was observed: Norman (Patourel (1971), Jewell (1996)), Chamavian, Thuringian, Saxon and Lombard (Nelson and Rio (2013) and Klapisch-Zuber et al. (1994, 177)) and Visigothic in Catalonia (Ros (2012) and Piniella del Valle (1986)).
In general, scholars advance the importance of defence to explain the rise of primogeniture and the exclusion of women. Bloch (1961, 200) relate the ubiquitous male preference in inheritance rules to military duties and Brenner (1985) reasons similarly. In fact, the core of the feudal system consisted in the exchange of means of maintenance for military aid, where men had a comparative advantage. However, inheritance rules usually did not completely exclude women from succession. Whenever a daughter inherited a landed estate, marriage customs took care of the seeming contradiction of a woman in charge of armies. Husbands took over the responsibility attached to the fiefdom, including wealth management, see Drell (2013). However, decision-making reverted to husbands as well, giving an impetus and incentive to younger sons to search for heiresses to marry and thus become part of the landed elite. In that sense, Holt (1985) indicates that an heiress “brought land to husband and ultimately to children” through inheritance. Marriages between inheritors from different countries were commonly used during the middle ages to increase estate size, see Habakkuk (1950), Clay (1968) and Girouard (1978).
According to Brenner (1985), population density reduced the benefits of primogeniture as interactions between individuals became more frequent and complex. The state replaced kinship in providing protection and law enforcement. Hence, the incentive to maintain large landholdings to provide expensive services reduced. English landlords were allowed to freely distribute land —with some restrictions— in 1540, and this was further extended in 1597. Similarly, Burgundy, Orléans and Moulins eased estate division around the same time. However, advances in terms of gender equality were slower. French revolutionaries introduced gender equality in inheritance during 1791, although the law was repealed during the First Empire. Nordic countries passed laws introducing equality during the second half of the 19th century, while Italy incorporated it in 1865. Succession to the throne of England and Scotland followed male-preference cognatic primogeniture until 2013, when it was changed to absolute primogeniture. However, the peerage still follows male-preference cognatic primogeniture. Other European kingdoms followed a similar transition during the 20th century: Sweden, the Netherlands, Norway, Belgium, Denmark and Luxembourg, moving away from a male-preferential treatment into absolute primogeniture. The institution of male-preference cognatic primogeniture still survives in Monegasque and Spanish royal succession laws.
7 The Marriage Market
On the marriage market, potential spouses sort candidates according to their wealth. Formally, let \(\mathcal{M}_{t}\subset\mathcal{L}_{t}\) be the set of manors that have a male heir and \(\mathcal{F}_{t}\subset\mathcal{L}_{t}\) be the set of manors that have a female heiress before marriages are arranged. Let \(\Psi\left(\text{·}\right)\) measure the relevant variable that determines marriages —for instance, wealth—, \(D\left(i,k\right)\) measure the distance between two potential spouses and let \(d_{t}>0\) be the threshold value during period \(t\). Finally, let \(\mu_{t}^{i,k}=1\) if there is a marriage between the male heir of manor \(i\in\mathcal{M}_{t}\) and the female heiress of manor \(k\in\mathcal{F}_{t}\), and \(\mu_{t}^{i,k}=0\) otherwise. The outcome of the marriage market is summarised in the following Proposition:
Proposition 5 The marriage market outcome described above is given by a set of \(\mu_t^{i,k}=\{0,1\}\) denoting marriages between heir \(i\) and heiress \(k\) such that aggregate valuations are maximised, each potential partner marries at most once or remains single and potential partners that marry are similar: \[\mu_{t}^{i,k}=\arg\underset{\mu_{t}^{i,k}}{\max}\sum_{i}\sum_{k}\left(\Psi\left(i\right)+\Psi\left(k\right)\right)^{2}\mu_{t}^{i,k},\] such that \(\forall i\in\mathcal{M}_{t},\,\forall k\in\mathcal{F}_{t}\) \(\mu_{t}^{i,k}=\left\{ 0,1\right\} ,\,\sum_{k}\mu_{t}^{i,k}\leq1,\,\sum_{i}\mu_{t}^{i,k}\leq1,\, \\ \mu_{t}^{i,k}D\left(i,k\right)\leq d_{t},\,\sum_{i}\sum_{k}\mu_{t}^{i,k}=\min\left\{ \left|\mathcal{M}_{t}\right|,\left|\mathcal{F}_{t}\right|\right\}.\)
Proposition 5 deserves some comments. First, the valuation for any given candidate is common to all potential partners. Equal valuation and functional super-modularity generate positive assortativeness. Constraints indicate that each potential couple is either married or not, individuals can only marry once, spouses must be close enough to marry and the total number of marriages equals the number of heirs or heiresses, whichever is smaller.
8 Country Unification
The model and the simulations predict, in general, a decrease in the number of manors over time. This holds true for countries like the present-day United Kingdom or France, which emerged as unified entities early. However, other regions like northern Italy and Germany witnessed a later process of unification, remaining fragmented for centuries, especially compared to neighbouring regions. This Section amends the model to reconcile it with the specific patterns observed in different regions.
Medieval northern Italy was formed by independent city-states ruled by local elites during the high and late middle ages. Conflicts among elites over control of a city were common and involved the use of violence, see Martines (1968). According to Hughes (1975, 7), medieval Genoa operated under “a system of long-lasting alliance within lineages and enmity between them [which] gave pattern to the seemingly pointless warfare played out on the streets of medieval Genoa and in its contado”. Lansing (2014) explains the case of Florence, where competition among lineages for the control of neighbourhoods was common and none achieved long-lasting supremacy. Similar conflicts arose in Venice, although according to Greif (1995), Venetians managed to reduce inter-clan tension through the mechanism they devised to choose the Doge. Remarkably, the city of Siena had to call Florence to help put an end to an internal riot between the Tolomei and Salimbeni families (Bowsky (1981, 166)). Finally, Jones (1965) also considers clan structures as a crucial aspect of the Italian middle ages: a clan acted together in all activities, especially for its defence.
From this evidence, we can presume that elites focused on gaining influence in their city. From the point of view of the model, we can associate a city-state with region \(\mathcal{L}\). Similarly, former manors can be represented by clans. The marriage market will show friction as well, since opposing clans’ heirs were not allowed to marry. Suppose that clans have similar initial conditions in terms of income \(Y\). According to the model, there will be minor changes in the distribution of wealth over time, as all clans will make similar war efforts. We can also expect similar marriages to be arranged within each opposing group. Thus, unification will be a lengthy process. The general model can be modified to accommodate clan rivalry on the marriage market by defining \(\mathcal{N}>1\) groups and assuming that marriages can only be arranged within each of these groups.
The Holy Roman Empire —the closest equivalent to Germany— presents a substantially different case. It was not a single country like France or England, but consisted of several principalities, duchies, counties and Free Imperial Cities, each ruled by a prince who enjoyed a large degree of autonomy. The Emperor’s succession was also different, insofar as the Holy Roman Empire elected the Emperor from its princes, instead of relying on some form of inheritance. To be elected as Emperor, a prince would have to convince his peers, usually through promises to grant them more rights. Therefore, the Emperor himself wielded little power within the empire in terms of capacity to intervene in state affairs, even lacking an imperial tax-system.45 Moreover, Holy Roman Empire princes practised partitioned inheritance, dividing the land among sons.46 These characteristics can be replicated in the model by setting \(\gamma=0,\) that is, certainty for a prince that his lineage will not rule in the next period. Accordingly, no investment in state-building or in the army is expected. This is partly consistent with reality: the Empire lacked an imperial tax-system and Ertman (1997, 237) indicates that only in 1450 did it begin building an administration as a response to outside pressure. \(\gamma=0\) also mean no military conquests. Indeed, inheritance —the Kingdom of Burgundy— and marriage —Italy— represented the largest territorial expansion mechanisms for the Empire. Lack of military growth is consistent with the organisation of the Empire, since neither the Emperor nor princes would have benefited from it: conquered lands would have been introduced as new states.
Despite the fact that the Empire as a whole only began to build a state relatively late, its princes were more willing to do so, see Evans and Wilson (2011, Ch. 4). A more efficient bureaucratic apparatus increased tax revenues that could then be used to raise an army. This was especially true for Savoy and Brandenburg, which tried to expand at the expense of weak neighbours. In the end, lack of unification through marriages between state heirs was a consequence of the inheritance policy. If the number of heirs exceeds two, marriages cannot counteract the multiplication of territorial units caused by partitioned inheritances. An additional feature of inheritances in the Holy Roman Empire was that they were calculated to avoid entailing to daughters, which exacerbated the effect by over-representing men on the marriage market.
References
Footnotes
The gender privileged by a given inheritance rule is irrelevant in our model. What is important is that both dynasties and landholdings descend through the same gender. However, we acknowledge historic customs.↩︎
Contrary to our findings, increasing levels of gender equality, broadly understood, induce economic growth in a pre-modern set-up, see Lagerlöf (2003). Insofar as state capacity is conducive to economic prosperity, our model indicates that gender discrimination, at least in some specific domains such as inheritance rules and for critical junctures, may be growth-enhancing.↩︎
His definition reads “the ability of the state to [...] coax compliant behaviour from the individuals”.↩︎
The role of state capacity as a lever to increase tax revenue to fund armies was early acknowledged by Bean (1973), Tilly et al. (1985) and Bonney (1999, 9).↩︎
Fighting for the control of scarce resources impacts other outcomes: fertility levels, with fatal consequences, in Croix and Dottori (2008) and education expenditure in Aghion et al. (2018). Economic development and industrialisation stifle war-making in Lagerlöf (2010), as industry reduces the need for land.↩︎
Complete female discrimination would imply choosing a brother or nephew as heir, who might change surname to continue the dynasty.↩︎
Persson and Tabellini (2004) document that more representative parliamentary and proportional democracies achieve higher state capacity when measured by government spending.↩︎
Kokkonen and Sundell (2014) find that countries where primogeniture was the inheritance system developed more, both in the past and in the present, than those that elected their ruler or applied agnatic seniority. Primogeniture avoided conflict because it clearly designated a young heir, delivering stability.↩︎
Debris (2005, 29) writes that “the risk of dynastic extinction was not to be taken lightly [...] because perpetuity was the [...] condition for the development of dynastic power”, own translation from French.↩︎
French Basques also circumvented the law to stick to primogeniture, see Arrizabalaga (2009). Similarly, the British fee tail institution aimed at preserving estates intact, see also Gobbi and Goñi (2018).↩︎
Several other accounts support the fear of lineage extinction. Clay (1968) details the case of the Marquess of Halifax, who disinherited his daughter and demanded that his heir adopt his family name. Payling (2001) describes a similar case within the Drayton family and notes that others married an heiress to a non-heir son while bequeathing to a male relative. Several wills clearly specify that heirs adopt the testator’s family name and bear arms unchanged, see Cokayne (1887). Hicks (1998, 32) summarises the idea simply: “preservation of the line and the family name really mattered”. Finally, Chu (1991) shows that primogeniture emerges as the optimal inheritance rule that minimises the risk of lineage extinction, see also references therein.↩︎
For instance, Maximilian I, Holy Roman Emperor, reflected at length on remarriage because he had only one son, see Debris (2005, 35). However, it is interesting to observe that genetic perpetuation had its own limits, as Debris (2005, 24–26) illustrates. In particular, the author observes that incumbent lords had high fertility rates. However, many of these children were forced to remain single, up to 40% of sons in some families, to “keep fiefdoms together”. Similar figures appear in Hurwich (1998). Appendix 6.1 rationalises this behaviour.↩︎
The Visigoths allowed women to inherit if parents died intestate and Burgundian codes favoured sisters over brothers when nubile girls died, see Drell (2013, 10).↩︎
Kotlyar (2018, 170) indicates that “preference for males was practically universal in feudal Europe reflecting the initial origin of fiefs”.↩︎
Inheritances transitioned from partitioned to intact. The model we develop does not consider the former case, but these were common in Britain before the Norman Conquest, in France under the Carolingians and for a while in the Holy Roman Empire, see Section 6.↩︎
By 1242, German princes embraced estate division. The practice lasted until the Thirty Years War. This “reckless division” (Cecil 1895) created more opportunities for war to break out, as well as a potential barrier to prosperity.↩︎
Gender-biased inheritance rules in favour of men may reflect the military origins of fiefs and the need to organise their defence. War is a prototypical male activity, and men are in general less risk-averse than women. This explains the extensive use of inheritance rules that preferentially select men. Moreover, to perpetuate dynastic continuity, surnames need to descend through the gender most likely to inherit landholdings. We conjecture that this delicate relationship may explain the joint prevalence of men as surname carriers and men being preferentially treated in inheritance rules.↩︎
Our model is quite simple regarding regional dynamics and predicts unification. Alesina and Spolaore (1997, 2006) model the optimal number of countries and its relation to state capacity and war.↩︎
Introducing endogenous fertility provides a margin that directly affects the probability of dynastic continuity under male-preference cognatic primogeniture. Although it may deliver interesting dynamics, the model is no longer tractable, as it introduces an endogenous discount rate. We refer the reader to Section 1 and Section 6 for a discussion about the importance of dynastic continuity.↩︎
For the sake of simplicity, the model disregards partitioned inheritances, which consisted in the division of an estate between siblings. Although historically relevant, the practice was progressively abandoned in favour of undivided inheritances, in particular primogeniture. Agency problems in managing large estates or marriage strategies may explain the practice of inheritance division. Furthermore, records indicate that children’s equal value also induced Lords to divide inheritances, see McNamara and Wemple (1973) and references therein. Introducing such practices would slow down the dynamics of the model but would not alter the qualitative results. Section 6 provides more information on the historical evolution of inheritance practices, and on the relationship between feudal obligations and the practice of primogeniture.↩︎
Other incentives for waging war may be related to fear of annihilation and family destruction and captivity. The model already accommodates the possibility of annihilation, represented by the extreme case of manor size going to zero. In particular, Section 3.1 proposes that tiny manors are completely obliterated during war. Although we do not explicitly model it, family destruction and captivity may be correlated to estate size. For the sake of simplicity, we abstract from these additional considerations. Historically, Strickland (2001) explains that during the medieval period knights and lords were typically spared, either for a ransom or out of mercy.↩︎
To accommodate this battle process which does not consider the distance to the battlefield, think of \(\mathcal{L}_{t}\) as a doughnut with manors on its surface and battles taking place in the central hole.↩︎
State capacity building fosters economic development by introducing market-supporting institutions, property rights and judicial systems. Here, for simplicity, the model does not capture this aspect. The introduction of such a mechanism would generate additional income for Lords that invest in state capacity, rewarding them. Furthermore, it would provide clear results relating state capacity to economic development through gender equality. However, this paper indirectly relates the two, although without the reinforcing effect that state capacity exerts through development.↩︎
Clearly, if there is only one manor it faces no risk of losing any territory due to an attack and its optimal number of soldiers is zero. However, assuming the externality is ignored, all manors will inevitably hire a positive number of soldiers and invest in state capacity if financially feasible.↩︎
Introducing labour input through commoners delivers the same qualitative results. Furthermore, allowing commoners released from productive labour activities to participate in war also yields similar results. In particular, under the linear specification \(Y_{t}^{i} = n_{t}^{i} - b_{t}^{i} + x_{t}^{i}\), where \(n_{t}^{i}\) are commoners and \(b_{t}^{i}\) represents those participating in war, results are qualitatively the same.↩︎
Lords historically used crop-sharing or leases to allocate production, see Slicher van Bath (1966). The burden supported by peasants varied between \(\frac{1}{2}\) and \(\frac{1}{3}\), depending on land fertility. Duby (1962) and Volokh (2009) find that share-cropping was more common in continental Europe while leasing was preferred in England.↩︎
No payments are required to maintain a certain level of state capacity once it is reached. However, results do not qualitatively change under a proportional tax farming system. In that case, tax income would be \((1-\psi)(1-\zeta)Y_{t}^{i}\frac{A_{t}^{i}+g_{t}^{i}}{1+A_{t}^{i}+g_{t}^{i}}\) where \(\zeta\in\left(0,1\right)\) represents the proportion of taxes officials keep as payment.↩︎
Under male-preference cognatic primogeniture, the probability of dynastic continuity equals \(1-0.5^{\Phi}\), where \(\Phi\) denotes the number of children. By increasing fertility, a Lord can partly insure himself against dynastic extinction.↩︎
Men and women are equally likely to inherit under a gender-egalitarian rule. Hence, equal numbers of men and women inherit land. Gender-biased rules over-represent one gender among land-inheritors and, consequently, fewer marriages between them can be arranged.↩︎
Such marriages also combined wealth and political power, which we do not incorporate in the model.↩︎
Removing small manors improves the numeric accuracy of the simulations. Indeed, Equation 2 and \(b_{t}^{i} > 0\) imply that no manor disappears due to conflict but they become infinitesimally small. At any rate, such tiny manors would be obliterated by more militarily capable rivals, and removing them is a natural step.↩︎
Marrying an heir to an heiress before the death of her father was a risky business, see Payling (2001). Arguably, waging war and deciding strategic alliances through pre-marital arrangements entailed a similar risk.↩︎
This particular sequence of events does not allow Lords to enter into treaties based on future marriages. Although relevant, that strategic aspect is not captured by the model and treaties are concluded in the aftermath of war. In any case, family bonds per se did not ensure peace among the parties. Charles the Bald’s conflicts with his brothers and nephew are good examples. Hicks (1998) explores the case of the Neville family, McLaughlin (1990, 199) cites the case of Richilde of Hainaut who fought her brother-in-law and Arnould III of Guînes who battled against his own son.↩︎
For instance, Bouchard (1981) explains the difficulties of early Capetians in finding suitable queens for their sons. Hurwich (1998) analyses the marriage pattern of the German lower nobility and finds that men tended to marry upwards on the social ladder, due to the way children from unequal marriages were treated. In Zeeland, there are records of marriages between spouses from different strata, but most marriages were arranged between spouses of similar rank, see Steensel (2012).↩︎
Alternatively, inheritors can be classified into \(\mathcal{N}>1\) groups according to their wealth. Only marriages between spouses who belong to the same group would be feasible.↩︎
Introducing endogenous fertility would not change the results for absolute primogeniture, because the gender of the heir is independent of number of children. However, it would introduce a strategic variable under male-preference cognatic primogeniture. Assuming a high enough cost of children, only wealthier Lords could secure dynastic continuity, thereby incentivising them for state-building and giving them an additional advantage during the war. We conjecture that qualitative results would remain similar, although probably the dynamics of male-preference cognatic primogeniture would be expedited.↩︎
English soldiers had a similar real cost, as compared to expenditure on nobles’ food, ranging between 0.428 for an archer and 2.57 for cavalrymen. The real cost of infantry was 1.14. Data on expenditures on food for nobles from Dyer (1989, 65) for the year 1380, and on wages from Norman and Pottinger (1979, 79).↩︎
The source says they received no less than 30 florins. One florin corresponded to 11 sous.↩︎
Ives (1983, 323) reports that a sergeant received £10 per circuit. This figure represents a real cost of 0.93. The real cost of an ordinary judge is estimated at 4.69. In Dyer (1989, 47), the real cost of a lawyer is 2.44.↩︎
Wealth also accumulates through war, but its outcome is similar for both regimes.↩︎
This follows from the fact that under this rule, the probability of observing a land-inheriting heir equals the probability of observing a land-inheriting heiress: absolute primogeniture means that the oldest sibling inherits. In contrast, under male-preference cognatic primogeniture, there are more land-inheriting sons than land-inheriting daughters. Consequently, few land-merging marriages can be arranged. Younger brothers seek an heiress to marry or enter alternative occupations, see Section 6 and footnote 13. When the number of participants in the marriage market tends to infinity, the ratio of marriages to participants approaches 0.5 under absolute primogeniture and 0.125 under male-preference cognatic primogeniture.↩︎
In that sense, the model predicts regional unification as manors merge. Section 8 explores two cases of late unification in the European context and proposes amendments to reconcile the model with these cases.↩︎
Hrdy and Judge (1993) are concerned about farmer families. However, the survival of elite members also depended on landholding size, as discussed above.↩︎
An Emperor’s revenue originated in the lands he controlled as a prince, a reason for which Johanek concludes that “the emperor was not really in a position to govern the Empire” (Hansen (2000, 21:295)).↩︎
The secular elector princes were forced to practise primogeniture to avoid land division, beginning from the Golden Bull of 1356, see Whaley (2012, 1:27).↩︎
Reuse
Citation
@online{roca_fernández2019,
author = {Roca Fernández, Èric},
title = {In the {Name} of the {Father:} {Inheritance} {Systems} and
the {Dynamics} of {State} {Capacity}},
volume = {25},
number = {4},
date = {2019-06-21},
doi = {10.1017/S1365100519000476},
langid = {en},
abstract = {This paper examines how the degree of
gender-egalitarianism embedded in inheritance rules impacts state
capacity at its early stages during medieval times. We present a
theoretical model in which building state capacity enables nobles to
raise taxes and overcome rivals. The model addresses the use of
inheritance to consolidate landholding dynasties, also accommodating
inter-state marriages between landed heirs. On the one hand,
dynastic continuity \—of utmost importance to European
medieval lords\— directly encourages statebuilding.
Male-biased inheritance rules historically maximise the likelihood
of dynastic continuity. We weigh this effect against the indirect
impact of the more frequent land merging marriages under
gender-egalitarian rules. Contrary to the literature, our results
suggest that gender-egalitarian norms —offering a low probability of
dynastic continuity— promote state capacity in the short run more
than gender-biased norms.}
}