Introduction

Pour comprendre les raisons qui ont amené à la création du modèle IS-LM, il est d’abord nécessaire de comprendre les limites du modèle qui le précédait : le modèle classique.¹

Notre point de départ est la crise de 1929 : après des années de croissance économique aux USA, beaucoup de ménages avaient investi dans la bourse (même en s’endettant). Entre le 24 et le 29 octobre 1929, la bourse de New York subit une crise boursière, avec des pertes de valeur de plus de 22%. Cette débâcle marqua le début de la Grande Dépression, une période de profond marasme économique qui mit en évidence les insuffisances du modèle classique pour expliquer et gérer les fluctuations économiques.

À la suite de cette crise boursière, la demande globale chuta drastiquement, entraînant une baisse significative de la consommation et de l’investissement. De nombreuses entreprises furent contraintes de fermer leurs portes, incapables de soutenir leur activité dans un environnement de demande réduite. Ce phénomène provoqua une augmentation massive du chômage, laissant des millions de personnes sans emploi. Le modèle classique, qui reposait sur l’hypothèse d’ajustements automatiques des marchés vers un équilibre naturel, ne parvenait pas à expliquer ni à remédier à ces déséquilibres prolongés. L’incapacité du modèle classique à fournir des solutions efficaces à la crise de 1929 a conduit les économistes à chercher de nouvelles approches pour comprendre et gérer les fluctuations économiques, ouvrant la voie à l’émergence du modèle IS-LM proposé par John Maynard Keynes.

Le modèle classique

Le modèle classique s’articule autour de trois équations fondamentales :²

• Équilibre dans le marché du travail
• Équilibre dans le marché de la monnaie
• Équilibre dans le marché de l’emprunt

Une idée clé du modèle classique est la croyance que les prix peuvent toujours s’adapter pour que la demande égalise l’offre dans n’importe quel marché. L’apport de Keynes à l’économie (d’où vient le modèle IS-LM) est l’idée contraire : dans le court terme, les prix sont fixes et ne changent pas. Ainsi, suite à un changement d’offre ou de demande, un nouvel équilibre réel est atteint.

Le marché de travail

Demande de travail

Les entreprises disposent d’une certaine quantité fixe de capital, qui est exogène au modèle. Elles maximisent leurs profits ($\pi$), qui dépendent du prix reçu par les ventes ($p \times Y$), du taux d’intérêt payé aux détenteurs de capital ($r$) et du salaire ($w$).

$$\pi = p Y - r \bar{K} - w N$$

où $\bar{K}$ est le stock de capital et $N$ est le nombre d’emplois. On suppose qu’une fonction de production transforme les inputs en outputs: $$Y = f(K, N) = F(\bar{K}, N)$$ Cette fonction de production montre des rendements décroissants dans chaque facteur de production:

• Quand on augmente $K$ ou $N$, la production augmente, mais de moins en moins.

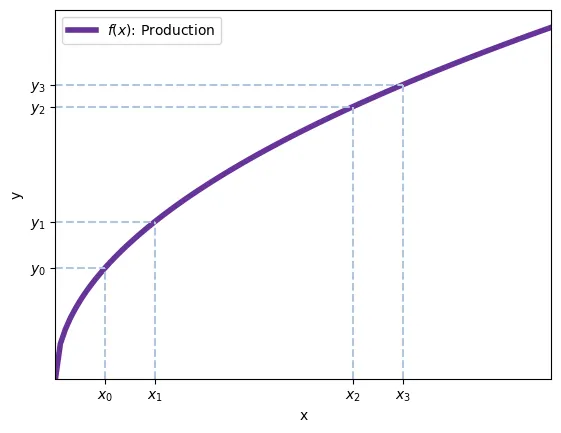
Ainsi, les entreprises maximisent en choisissant le nombre de travailleurs, car elles ne peuvent pas affecter ni le prix, ni le taux d’intérêt ni le salaire : $$\max_{N} \pi = p F(\bar{K}, N) - r \bar{K} - w N$$

La condition de premier ordre maximisant les profits est :

$$\frac{\partial \pi}{\partial N} = p F_{N}(\bar{K}, N) - w = 0$$

Si on réarrange, on obtient l’équation de demande de travail :

$$F_{N}(\bar{K}, N) = \frac{w}{p}$$

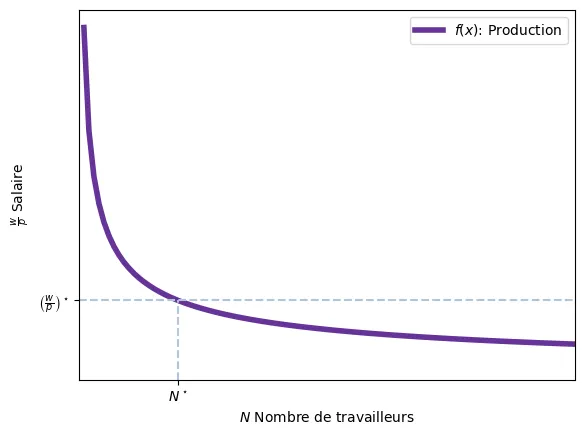
Autrement dit, la demande de travail $N^d$ est une fonction décroissante du salaire réel $\frac{w}{p}$. Nous la notons, de manière générale avec, $N^d = f\left(\frac{w}{p}\right)$

De plus, avec un certain nombre de travailleurs $N$, on retrouve le salaire d’équilibre $\left(\frac{w}{p}\right)^\star$ Ainsi, si le nombre de travailleurs augmente, le salaire diminue.

Exemple

Imaginons que l’économie dispose de 4 unités de capital ($\bar{K} = 4$), et que la fonction de production est $F(\bar{K}, N) = \bar{K}^{0.5} N^{0.5} = 2 N^{0.5}$ Les entreprises maximisent leurs profits:

\begin{align} \max_{N} \pi &= p F(\bar{K}, N) - r \bar{K} - w N \\ \max_{N} \pi &= p 2 N^{0.5} - r \bar{K} - w N \\ \frac{\partial \pi}{\partial N} &= p N^{-0.5} - w = 0 \\ N^d &= \left(\frac{p}{w}\right)^2 = \left(\frac{w}{p}\right)^{-2} \\ \end{align}

Offre de travail

Les travailleurs offrent du travail pour gagner un salaire avec lequel acheter des biens et services. En travaillant, ils renoncent au temps de loisir. Ainsi, les travailleurs arbitrent entre le temps de loisir et ce qu’ils peuvent acheter avec le salaire:

• Si $w$ augmente, l’offre de travail augmente car chaque heure travaillée paie plus
• Si $p$ diminue, l’offre de travail augmente car les biens sont moins chers.

Enfin, l’offre de travail est représentée par la fonction croissante $N^s = g\left(\frac{w}{p}\right)$

Équilibre

Pour un niveau de salaire réel $\frac{w}{p}$, les entreprises embauchent des travailleurs selon $N^d=f\left(\frac{w}{p}\right)$. Pour le même salaire réel, l’offre de travail venant des travailleurs est $N^s=g\left(\frac{w}{p}\right).$

L’équilibre est atteint lorsque $N^d=N^s$ Ainsi, selon le modèle classique:

• La technologie et les préférences des travailleurs déterminent le salaire réel.
  • La technologie affecte la fonction de production, et cela affecte la dérivée $F_{N}$.
• Une fois le nombre de travailleurs d’équilibre connu, cela implique un niveau de production dans l’économie.
  • Avec $N^\star$, la fonction de production nous donne le PIB: $Y^\star = F(\bar{K}, N^\star)$

Implications pour la Grande Dépression

Lors de la Grande Dépression, on constatait des réductions du PIB d’environ 30%. C’est massif. En même temps, le salaire réel augmentait (peu) car le niveau de prix $p$ avait baissé plus que les salaires $w$. Pour un économiste classique, seule une option était possible pour expliquer cela: les préférences des travailleurs avaient changé et, maintenant, ils préféraient travailler moins.

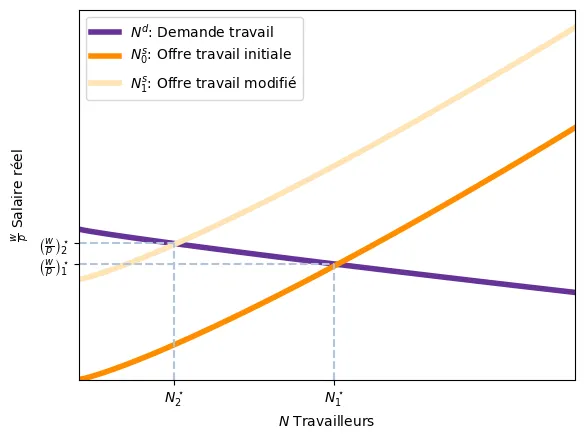
Comme $N$ se réduit, la production diminue car $Y = F(\bar{K}, N)$.

Marché de la monnaie

Demande de monnaie

On s’appuie sur la théorie quantitative de la monnaie d’Alfred Marshall pour expliquer pourquoi les gens détiennent des encaisses réelles.

Selon Marshall, les agents économiques ont besoin d’encaisses réelles pour financer leurs achats. Ainsi, la demande de monnaie est proportionnelle au PIB. De plus, on peut utiliser un même billet de multiples occasions: la monnaie a une vitesse $v.$ Plus la monnaie est rapide, moins le besoin d’encaisses est nécessaire car le même billet peut être utilisé pour financer plusieurs transactions. Enfin, si le niveau de prix $p$ est plus important, il est nécessaire de détenir plus de monnaie.

$$M^d = v p Y$$

Offre de monnaie

Ceci est simple : la banque centrale mets en circulation un certain nombre de billets.

$$M^s = \bar{M}$$

Équilibre

L’équilibre est atteint lorsque $M^d = M^s$. Autrement dit:

$$p = \frac{1}{v \bar{Y}} \bar{M}$$

Ici, nous avons mis $\bar{Y}$ car le niveau de production est déterminé par la fonction de production et le nombre de travailleurs et donc, est exogène au marché de la monnaie. On retrouve la pensée classique : le niveau de prix s’ajuste de manière à ce que l’offre de monnaie soit égale à la demande de monnaie.

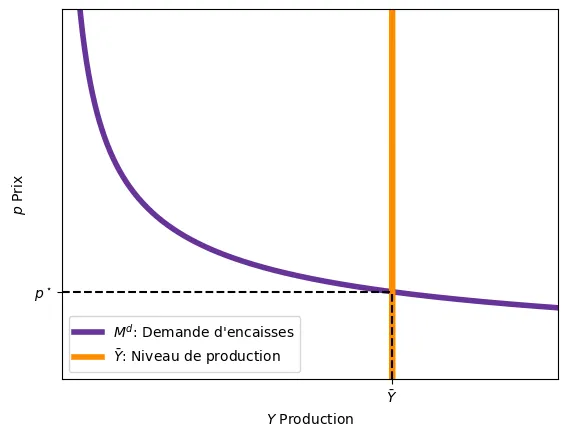
Imaginons que la banque centrale décide d’augmenter l’offre de monnaie.

• Celui-ci ne va pas affecter la production $Y$ car elle est déjà déterminée.
  • Note: dans le modèle IS-LM, un changement de $M$ change la production d’équilibre.
• Comme les gens disposent de plus de monnaie, ils souhaitent faire plus d’achats, mais comme la production est fixe, cette hausse dans la demande se traduit par une augmentation des prix.
  • Ainsi, on retrouve un nouvel équilibre avec un niveau de prix plus élevé.

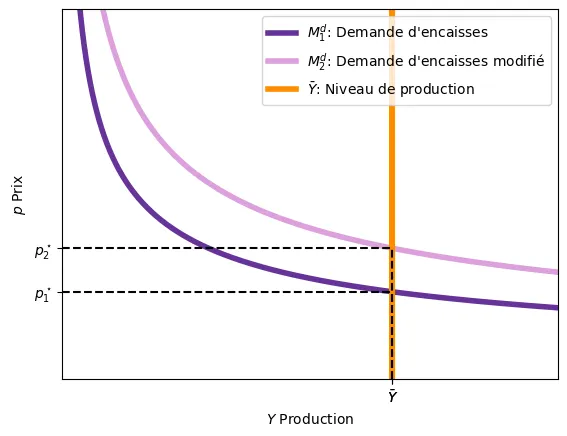
Implications

L’implication principale qu’on peut tirer du marché de la monnaie est que toute augmentation de l’offre monétaire engendre de l’inflation. En effet, à partir de l’équation nous avons:

$$p = \frac{1}{\bar{v}\bar{Y}} \bar{M} \implies \gamma_p = \gamma_M - \gamma_Y$$ où $\gamma$ indique le taux de croissance. Ainsi, le taux de croissance des prix ($\gamma_p$, l’inflation) est égal au taux de croissance de la masse monétaire ($\gamma_M$) moins le taux de croissance du PIB ($\gamma_Y$).

Les économistes Pedro Teles, Harald Uhlig et João Valle e Azevedo se sont intéressés à vérifier si, en effet, les augmentations d’offre monétaire généraient de l’inflation (une fois escompté la croissance du PIB). Selon le schéma ci-dessous, notre théorie quantitative de la monnaie est assez acceptable (voir https://doi.org/10.1111/ecoj.12336)

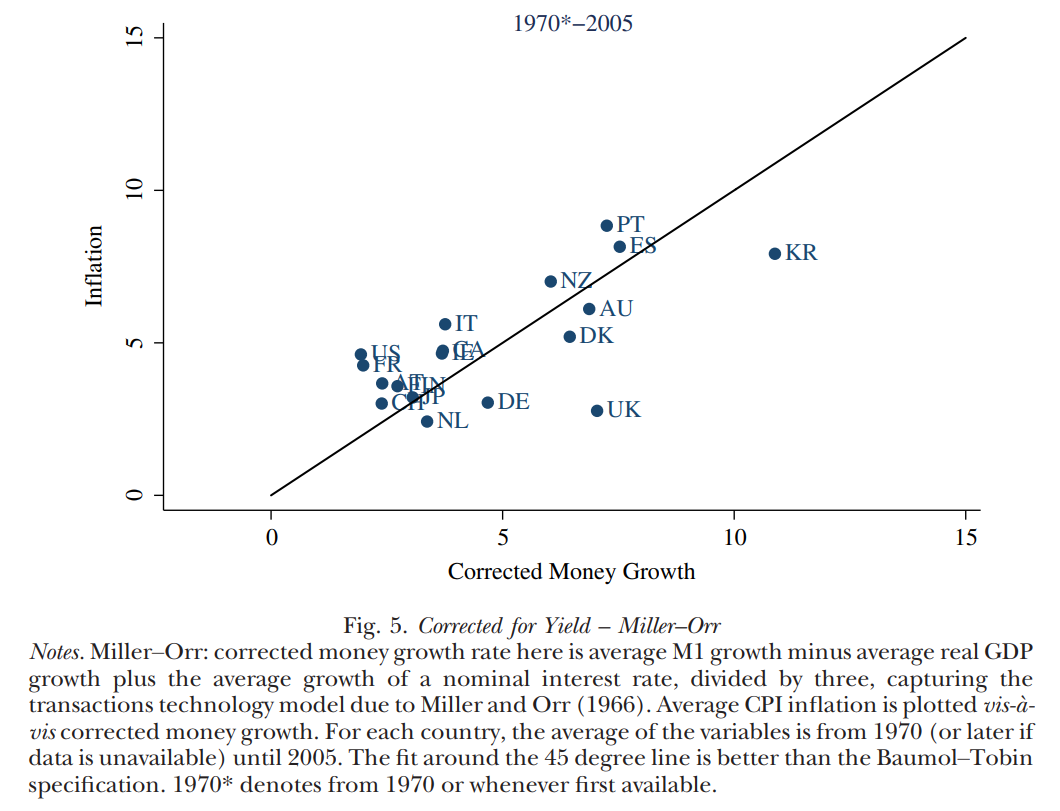
L’équation indiquant la quantité de monnaie que les individus souhaitent détenir est $p = \frac{1}{\bar{v}\bar{Y}} \bar{M}$ Une idée centrale de la pensée classique est que les prix s’ajustent immédiatement. Autrement dit, une hausse de l’offre monétaire n’a pas d’effet sur le PIB ($\bar{Y}$) car celui-ci est déterminé par le marché du travail et la courbe de production. Bien sûr, avoir plus de monnaie ne change aucune de ces deux courbes! Donc, si le PIB est incapable de réagir, et si nous imaginons que la vitesse de la monnaie reste constante, la seule chose qui se passe est que les gens détiennent plus de monnaie dans leurs poches. Par conséquent, ils sont prêts à l’utiliser pour faire des achats, ce qui produit il existe une augmentation de la demande des biens. Mais, comme nous avons dit, la production ne change pas. Ainsi, cette demande accrue se traduit par une augmentation des prix.

Note: le modèle IS-LM (et l’économie Keynésienne) s’opposent à l’hypothèse que la quantité produite ne peut pas s’ajuster.

Marché de l’emprunt

La dernière composante du modèle classique est le marché de l’emprunt. Ce marché détermine le taux d’intérêt d’équilibre. Comme nous le verrons, ce marché n’a pas d’impact sur les autres variables. Le taux d’intérêt se détermine entièrement à partir des autres variables que nous connaissons déjà.

Le point de départ est l’identité comptable indiquant que, tout ce qui est produit dans une économie, doit être:

• Acheté par les ménages
• Utilisé comme investissement (emprunt)
• Acheté par le gouvernement

Ainsi :

$$Y = c(Y-\bar{T}) + I(r) + \bar{G}$$

Nous voyons que la consommation est une fonction du revenu disponible, c’est-à-dire, le revenu total moins les impôts : $c(Y-\bar{T})$. L’investissement est une fonction du taux d’intérêt, et les dépenses du gouvernement sont exogènes, comme le niveau d’imposition.

Offre de fonds prêtables

Une autre manière de présenter la même équation est de considérer que que l’investissement doit être égal à l’épargne totale. En effet, tout ce qui est produit mais non-consommé est épargné. Ce sont les fonds prêtables. Si pour n’importe quelle raison ils augmentent, les épargnants se concurrencent pour les placer auprès des entreprises, faisant diminuer le taux d’intérêt. Et à l’inverse, si les entreprises ont besoin d’investir davantage (pour un même niveau d’épargne), elles offriront un taux d’intérêt plus important pour attirer l’épargne des ménages.

• Note: on peu imaginer que la consommation des ménages dépende aussi du taux d’intérêt, mais ceci n’est pas essentiel.

De manière mathématique, l’épargne totale est la somme de l’épargne des ménages plus l’épargne du gouvernement

• Le gouvernement normalement a une épargne négative car il est en déficit.

Si l’on dénote l’épargne privé par $S^P$ et l’épargne publique par $S^G$

$$S^P = Y - \bar{T} - c(Y - \bar{T})$$ $$S^G = \bar{T} - \bar{G}$$

Et donc, l’épargne total $S = S^P + S^G$ devient

\begin{align} S &= S^P + S^G = \\ &= Y - \bar{T} - c(Y - \bar{T}) + \bar{T} - \bar{G} = \\ &= Y - c(Y-\bar{T}) - \bar{G} \end{align}

Veuillez noter que les impôts réduisent l’épargne privée et augmentent l’épargne publique. En fait, les impôts sont un transfert de ressources entre les individus et le gouvernement.

Ainsi, pour nous, l’offre de fonds prêtables est une droite verticale : elle dépend uniquement de la production $Y$ qui est fixe, des impôts (exogènes) et des dépenses publiques (exogènes).

Demande de fonds prêtables

La demande de fonds prêtables est une fonction décroissante du taux d’intérêt. En effet, les entreprises doivent rembourser leurs emprunts et, si le taux augmente, elles préfèrent ne pas emprunter autant.

Si l’on place l’offre et la demande sur un même schéma, on obtient l’équilibre du marché. En effet, si nous partons de $Y = c(Y-\bar{T}) + I(r) + \bar{G}$, nous avons :

\begin{align} Y &= c(Y-\bar{T}) + I(r) + \bar{G} = \\ &= \bar{T} - \bar{T} +c(Y-\bar{T}) + I(r) - \bar{G} \end{align} \begin{align} Y - \bar{T} + \bar{T} - c(Y-\bar{T}) - \bar{G} &= I(r) \\ Y - \bar{T} - c(Y-\bar{T}) + \bar{T} - \bar{G} &= I(r) \\ \overbrace{Y - \bar{T} - c(Y-\bar{T})}^{S^P} + \overbrace{\bar{T} - \bar{G}}^{S^G} &= I(r) \\ S^P + S^G &= I(r) \\ S = I(r) \end{align}

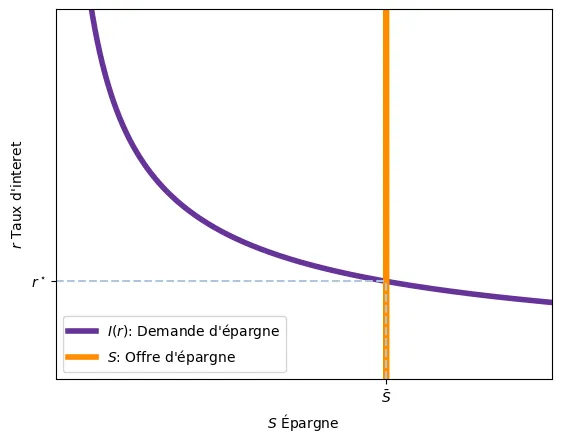
Si le gouvernement décide d’augmenter ses dépenses publiques $G$, l’offre de fonds prêtables diminue, car $S = Y - c(Y-\bar{T}) - \bar{G}$. Ainsi, avec moins de fonds disponibles, leur prix d’équilibre (le taux d’intérêt) augmente.

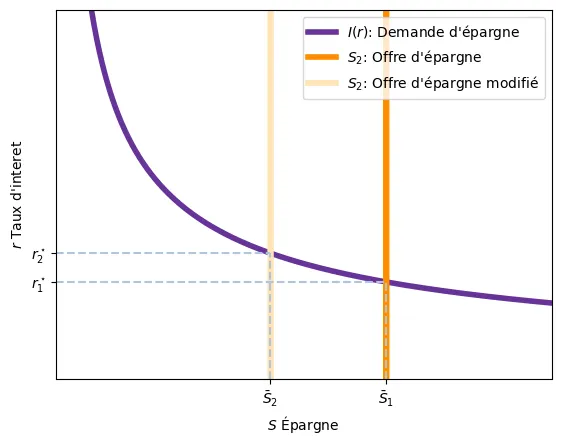
Synthèse

Selon le modèle classique, les trois marchés déterminent l’état de l’économie.

Ainsi, le marché de travail détermine le salaire réel $\frac{w}{p}$ et le nombre de travailleurs $N^\star$. Une fois le nombre de travailleurs connu, la fonction de production indique l’offre global de biens: $\bar{Y} = F(\bar{K}, N^\star)$. Enfin, le marché de la monnaie ajuste le prix $p$ pour que l’offre de monnaie coïncide avec le niveau de production (en considérant la vitesse). Avec $p$, le salaire nominal est aussi établi : $w = \frac{w}{p} \times p.$ De l’autre côté, avec $\bar{Y}, \bar{T}$ et $\bar{G}$, et la fonction de demande d’épargne, nous pouvons calculer le taux d’intérêt.

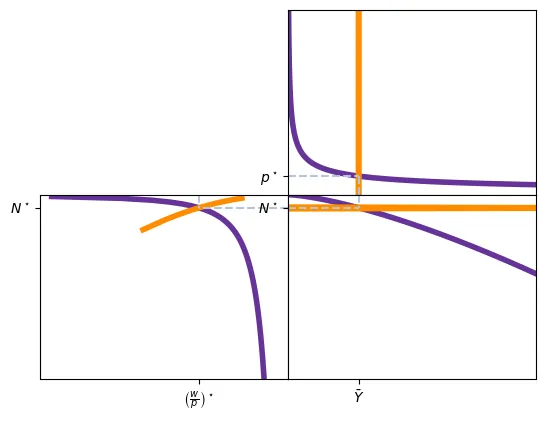
Politique budgétaire et monétaire

Dans le modèle classique, les politiques budgétaire et monétaire ne permettent pas d’augmenter la production ou de réduire le taux de chômage. Le seul effet est de changer le taux d’intérêt ou le niveau de prix.

Augmentation des dépenses publiques

Imaginons que le gouvernement souhaite augmenter les dépenses publiques pour stimuler la demande et permettre une sortie plus rapide d’une crise. Selon le paradigme classique, cette hausse de dépenses n’a aucun impact sur le PIB (ni sur les autres variables réelles).

En effet, $G$ apparaît seulement dans l’équation d’équilibre du marché de l’emprunt. Plus en détail, elle fait partie de l’offre de fonds prêtables:

$$S = S^P + S^G = \bar{Y} - c(\bar{Y}-\bar{T}) - \bar{G}$$ Ici, j’indique $\bar{Y}$ pour signaler que cette variable est fixe. En effet, le niveau de production se détermine par l’offre et demande de travail sur le marché de l’emploi. Ainsi, si $G$ augmente, immédiatement:

• Soit $C$ diminue et $S$ reste inchangé
• Soit $C$ demeure constant, $S$ diminue et, donc, l’investissement diminue.

On appelle à ce phénomène effet d’éviction (crowding out). En augmentant ses dépenses, le gouvernement “prend” de l’argent aux individus, ce qui se traduit par une moindre consommation ou une réduction de l’investissement. L’effet d’éviction est l’un des arguments justifiant la forte opposition des économistes classiques à l’État providence:

• Une réduction de l’investissement implique moins de capital demain, donc moins de croissance économique. Pour rappel: $Y=F(K,N)$
• La consommation peut baisser. En effet, les agents économiques sont considérés comme plus à même de dépenser de manière optimal leur revenu que ce que l’État pourrait le dépenser.

Augmentation de l’offre de monnaie

Nous avons vu qu’une hausse de l’offre monétaire implique que la courbe de demande de monnaie se déplace vers le haut, car

$$p = \frac{1}{\bar{v}\bar{Y}} \bar{M}$$

En conclusion, le seul effet d’une politique monétaire expansionniste est de faire monter le niveau des prix, sans aucun impact sur la production.

Quoi faire face à la crise de 1929 ?

Selon un économiste classique, rien! Il dirait: “Regardez, je vois que beaucoup de personnes ne travaillent pas. Cela signifie que soit la fonction de production a changé, soit que les préférences des individus ont changé. Si c’était un changement technologique, le salaire réel aurait baissé, et nous n’observons pas ça. Ce qu’on observe, c’est une hausse du salaire réel : l’offre de travail a diminué! Cela explique aussi que la production diminue, et que les prix chutent, comme on le voit.

Comme tout ce qu’on observe est le résultat d’un processus d’optimisation individuelle qui conduit les individus à préférer travailler moins, on ne doit rien faire. Et en plus, si on augmentait les dépenses publiques ou l’offre de monnaie, le seul effet serait sur des variables nominales.”

Exercises

Problem Set 1: Classiques