“Je soutiendrai que les postulats de la théorie classique ne sont applicables qu’à un cas particulier et non au cas général. […] De plus, les caractéristiques du cas particulier supposé par la théorie classique ne sont pas celles de la société économique dans laquelle nous vivons réellement, ce qui fait que son enseignement est trompeur et désastreux si nous tentons de l’appliquer aux faits de l’expérience.” – John Maynard Keynes

Introduction

À différence du modèle classique, le modèle IS-LM proposé par John Maynard Keynes indique qu’une faible demande agrégée peu être la cause derrière la crise de 1929, y compris le taux de chômage. En effet, pour Keynes le problème principal du modèle classique était l’ajustement presque que immédiat de tous les prix pour égaliser l’offre et la demande. Pour lui, l’offre totale ne suffit pas à elle tout seule à déterminer la production nationale. La théorie Keynésienne explique les fluctuations économiques par les changements de la demande agrégée.

Le modèle IS-LM donc, change une hypothèse basiques dans le modèle classique: les prix sont flexibles. Selon Keynes, au moins à court terme, les prix sont fixes. Cette modification mineure aura des profondes répercutions: les modifications de $M$, $G$ et $T$ engendrent des changements d’output. Ceci ouvre la porte à des interventions publiques pour limiter les effets des crises. De plus, le taux de chômage devient involontaire Pour rappel, pour les classiques tout chômage est volontaire car les individus offrent leur travail de manière optimale.

Le modèle IS-LM s’appuie sur deux équations: IS (équilibre dans le marché de l’emprunt) et LM (équilibre dans le marché de la monnaie). Nous les aborderons l’une après l’autre.

La courbe IS

Le point de départ pour concevoir la courbe IS est l’équilibre dans le marché de l’emprunt (ou le marché des biens, c’est le même). L’équation initiale est la même que les classiques utilisaient:

$$Y = c(Y-T) + I(r) + \bar{G}$$

Remarques

Même si l’équation paraît identique, certaines différences majeurs s’y cachent.

En premier lieu, selon Keynes la demande détermine le niveau de production. Cela veut dire que le niveau $Y$ s’ajuste à la demande de manière à ce que production et demande s’égalisent. Ainsi, si $\bar{G}$ change, $Y$ change; si $T$ change, la consommation change et, donc, $Y$ change, etc. Ceci est en opposition aux classiques: pour eux, $Y$ est déterminé par la production: $Y = F(\bar{K},N)$. Ce niveau est immodifiable sauf si $\bar{K}$, $N$ ou $F$ changent.

Le fait que dans le système économique Keynésienne les changements de $G$ et $T$ aient des effets sur le niveau de production ouvre la porte aux interventions de l’état et nous invite à penser aux impacts de l’effet multiplicateur des dépenses publiques et des réductions d’impôts.

Dans le modèle classique, certains auteurs introduisent le taux d’intérêt dans la consommation, disant qu’un taux plus élevé favorise l’épargne au détriment de la consommation. Pour simplifier, nous avions ignoré $r$ dans la fonction de consommation.

Selon Keynes, la demande de biens et services ne changeait pas avec le taux d’intérêt et il décida de ne pas modéliser la consommation comme une fonction du taux d’intérêt.

Finalement, Keynes pensait que les fluctuations économiques venaient des changements dans la fonction d’investissement: les investisseurs (entreprises) pensant que les rendements allaient diminuer ajustent leur demande de fonds prêtables à la baisse (pour un taux $r$ donné). En effet, il n’avait pas tort : l’investissement est beaucoup plus volatil comparé à la consommation.

Année	$\frac{I}{Y}$(%)	$\frac{C}{Y}$(%)
1955	17.1	63.5
1958	13.8	64.5
1973	16.1	62.6
1975	12.5	64.0
1979	16.0	62.7

Pour revenir à la Grande Dépression, en 1929 le niveau d’investissement par rapport au PIB aux USA était 15.7%, tandis qu’en 1933 il chuta à 2.5%. Cela reflète bien le manque de confiance des investisseurs dans la trajectoire de l’économie en 1933.

La fonction de consommation

La fonction de consommation Keynésienne se base sur deux idées:

• Il existe un niveau de consommation incompressible $c_0$ qui est le niveau minimal nécessaire pour la survie. Ce concept souligne que, même si le revenu des ménages diminue, il existe un niveau de consommation en dessous duquel les ménages ne peuvent pas descendre sans compromettre leur bien-être de base. Par exemple, les dépenses pour la nourriture, le logement et les soins de santé sont souvent considérées comme incompressibles.
• La propension marginale à consommer (PMC) comprise entre 0 et 1. Ce concept est crucial pour comprendre comment les variations du revenu affectent la consommation. Si la PMC est élevée (proche de 1), cela signifie que les ménages consomment une grande partie de leur revenu supplémentaire. Si la PMC est faible (proche de 0), cela signifie que les ménages épargnent une grande partie de leur revenu supplémentaire.

Enfin, Keynes indique le niveau de revenu de référence pour les décisions des ménages est le revenu net d’impôts. Ceci est logique car, si le niveau d’imposition est très élevé, une augmentation du revenu reviendrait à une augmentation quasi nulle des ressources disponibles et, donc, les ménages ne pourraient pas consommer davantage.

Ainsi, la fonction de consommation Keynésienne peut être représentée mathématiquement par l’équation suivante :

$$C = c_o + c_1 (Y-T)$$

où $c_0 > 0$ est la consommation incompressible et $c_1 \in (0,1)$ est la PMC.

L’effet multiplicateur

Une caractéristique importante de la pensée de Keynes est que le gouvernement peut stimuler l’économie en menant des interventions publiques. Cette idée donne lieu au concept de multiplicateur Keynésienne qui indique de combien le PIB augmente quand le gouvernement augmente $G$ d’une unité ou réduit $T$ d’une unité.

Comme dans l’économie Keynésienne la production totale est définie par la demande, nous pouvons nous intéresser au changement du PIB suite à une augmentation de $G$ ou une réduction de $T$.

Mathématiquement, l’effet multiplicateur des dépenses publiques est:

$$\frac{d Y}{d G}$$

tandis que celui lié aux impôts est

$$\frac{d Y}{d T}$$

Multiplicateur des dépenses publiques

Pour calculer comment une augmentation de $G$ de $\Delta G$ augmentera le PIB, nous pouvons procéder par étapes.

1. Changement initiale des dépenses = $\Delta G$
2. Cela augmente $Y$ de $\Delta G$
3. L’augmentation de $Y$ implique le revenu disponible pour les ménages augmente de $\Delta G$ et, donc, leur consommation augmente de $PMC \Delta G$
4. Le changement de $C$ implique une hausse de $Y$ de $PMC \Delta G$
5. Ce nouveau changement de $Y$ augmente, à nouveau, le revenu disponible. La consommation augmente de $PMC PMC \Delta G = PMC^2 \Delta G$
6. Etc.

Mis ensemble, l’effet total de $\Delta G$ est de faire augmente le $Y$ de $\Delta Y = \Delta G + PMC \Delta G + PMC^2 \Delta G + PMC^3 \Delta G + \ldots$. Ainsi, le multiplicateur des dépenses publiques est:¹

\begin{align} \frac{\Delta Y}{\Delta G} &= 1 + PMC + PMC^2 + PMC^3 + \ldots = \\ &= \frac{1}{1-PMC} = \\ &= \frac{1}{1-c_1}> 1 \end{align}

Une manière alternative (et plus mathématique) de le calculer est de prendre la dérivée totale de $Y = c_0 + c_1 (Y-T) + I(r) + G$ par rapport à $Y$ et $G$:

\begin{align} \mathrm{d}Y &= c_1 \mathrm{d} Y + \mathrm{d} G \\ (1-c_1) \mathrm{d} Y &= \mathrm{d} G \\ \frac{\mathrm{d}Y}{\mathrm{d}G} &= \frac{1}{1-c_1} \end{align}

Exemple

Si l’on suppose une propension marginal à consommer $c_1 = 0.6$, le multiplicateur des dépenses publiques est égal à

$$\frac{\Delta Y}{\Delta G} = 1 + 0.6 + 0.6^2 + 0.6^3 + \ldots = \frac{1}{1-0.6} = 2.5$$

Dans notre exemple, une augmentation de $G$ de 1 euro augmente le revenu (PIB) d’équilibre de 2.5 euros.

Multiplicateur des impôts

De manière analogue au multiplicateur des dépenses publiques, l’effet multiplicateur des impôts vient du fait qu’une baisse d’impôts augmente le revenu disponible $Y-T$. Cette augmentation impactera positivement la consommation, qui augmentera à son tour le revenu $Y$, qui augmentera le revenu disponible, etc.

Pour le voir, nous allons calculer l’effet d’une augmentation de $T$ de $\Delta T$ et constater la réduction que cela implique pour le PIB. Bien sûr, une réduction d’impôts aura l’effet inverse. D’abord, augmenter les impôts de $\Delta T$ réduit $Y$ de $PMC \Delta T$.² Cette diminution de $Y$ implique que le revenu disponible se réduit de $PMC \Delta T$ et, ainsi, la consommation chute de $PMC PMC \Delta T = PMC^2 \Delta T$. L’effet total est:

\begin{align} \frac{\Delta Y}{\Delta T} &= - PMC - PMC^2 - PMC^3 - \ldots = \\ &= -\frac{PMC}{1-PMC} = \\ &= -\frac{c_1}{1-c_1} < 0 \end{align}

De manière similaire, si $Y = c_0 + c_1 (Y-T) + I(r) + G$, et que nous dérivons par rapport à $Y$ et $T$:

\begin{align} \mathrm{d}Y &= c_1 \mathrm{d} Y - c_1 \mathrm{d} T \\ (1-c_1) \mathrm{d} Y &= - c_1 \mathrm{d} T \\ \frac{\mathrm{d}Y}{\mathrm{d}T} &= - \frac{c_1}{1-c_1} \end{align}

Si, au lieu d’augmenter les impôts nous les diminuons, le PIB augmentera de $\frac{c_1}{1-c_1}.$

Exemple

Si l’on suppose une propension marginal à consommer $c_1 = 0.6$, l’effet multiplicateur des impôts est:

$$\frac{\Delta Y}{\Delta T} = - \frac{0.6}{1-0.6} = - 1.5$$

---

La courbe IS relie le niveau de production d’équilibre et le taux d’intérêt. Parce que le taux d’intérêt représente le coût de l’emprunt pour financer des projets d’investissement, une augmentation du taux d’intérêt réduit l’investissement. Par conséquent, la fonction d’investissement est décroissante avec $r$:

$$I = I(r)$$

La courbe IS représente l’équilibre dans le marché de l’emprunt. L’épargne (offre de fonds prêtables) est la somme de l’épargne publique et privé. L’épargne publique est la différence entre $T$ et $G$, tandis que l’épargne privé est la différence le revenu net d’impôts $Y-T$ moins la consommation $C.$

$$S = S^G + S^P = \overbrace{\bar{T} - \bar{G}}^{S^G} + \overbrace{Y - \bar{T} - C(Y-\bar{T})}^{S^P} = Y - C(Y-T) - \bar{G}$$

L’équilibre dans ce marché implique:

$$I(r) = S = Y - C(Y-T) - \bar{G}$$

Sur le plan $(Y-r)$, la courbe IS est décroissante avec une pente égale à:

$$I^\prime \mathrm{d}r = (1-c_1) \mathrm{d}Y \implies \frac{\mathrm{d}r}{\mathrm{d}Y} = \frac{1-c_1}{I^\prime} < 0$$

car $I^\prime < 0$ parce que l’investissement se déduit avec le taux d’intérêt.

Par exemple, si on pose que $I(r) = \frac{1}{r}$ et $c_0 = 10$, $c_1 = 0.6$, $\bar{T} = 3$ et $\bar{G} = 8$, nous avons

\begin{align} Y &= 10 + 0.6 (Y-3) + \frac{1}{r} - 8 \\ Y &= 0.2 + 0.6 Y + \frac{1}{r} \\ 0.4 Y &= 0.2 + \frac{1}{r} \\ 0.4 Y - 0.2 &= \frac{1}{r} \\ r &= \frac{1}{0.4Y - 0.2} = \frac{5}{2Y - 1} \end{align}

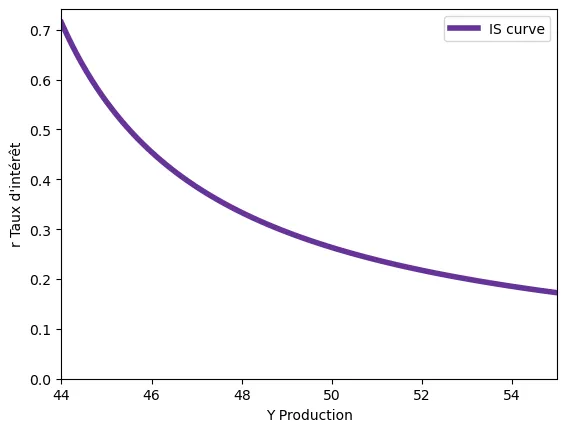
Une manière plus mathématique de vérifier que la courbe IS est décroissante (sur le plan $(Y-r)$) est de prendre la dérivée de $r$ par rapport à $Y$, c-est-à-dire, analyser si $r$ augmente ou diminue quand $Y$ augmente.

\begin{align} Y &= \overbrace{C(Y,T)}^{c_0 + c_1(Y-T)} + I(r) + \bar{G} \implies \\ \mathrm{d}Y &= c_1 \mathrm{d}Y + I^\prime \mathrm{d}r \\ (1-c_1) \mathrm{d}Y &= I^\prime \mathrm{d}r \\ \frac{\mathrm{d}r}{\mathrm{d}Y} &= \frac{1-c_1}{I^\prime} < 0 \end{align}

Ainsi, quand $Y$ augmente, $r$ diminue.

Déplacements de la courbe IS

La courbe IS est une relation entre $Y$ et $r$ que l’on trace pour certaines valeurs de $T$ et $G$. Autrement dit, la partie IS est en réalité une relation à quatre dimensions: $Y, r, T, G$ et nous en fixons deux pour pouvoir le tracer sur un plan. Par conséquent, si les variables hors de nos axes ($T$ et $G$ ici) varient, cela veut dire que nous sommes dans une autre zone de la courbe à quatre dimensions. Comment cela se manifeste sur notre plan à deux dimensions $(Y,r)$?

Augmentation de $G$

Imaginons que $G$ augmente. Notre relation de départ est:

$$Y = C(Y,T) + I(r) + \bar{G}$$

Si $G$ augmente, l’équation n’est plus vérifiée et quelque chose doit changer pour restaurer l’égalité.

Pour nous faciliter le travail, on pense de la manière suivante: pour une valeur de $Y$, est-ce que $r$ doit augmenter ou diminuer pour restaurer l’équilibre? Graphiquement, cela revient à se demander : est-ce que la courbe IS se déplace vers le haut ou vers le bas? Analysons cette première possibilité: pour un niveau de $Y$ donné, la côté droit de l’équation a augmenté car $G$ a augmenté. $Y = C(Y,T) + I(r) + \uparrow\bar{G}$

Ainsi, le côté gauche ne peut pas changer, car nous analysons le changement pour un niveau $Y$ donné, et donc, constant. Pour rétablir l’équilibre, la seule possibilité est que $I(r)$ diminue.

$Y = C(Y,T) + \downarrow I(r) + \uparrow\bar{G}$

Et, pour réduire $I(r)$, $r$ doit augmenter.

En conclusion, si $G$ augmente, pour un niveau donné de $Y$,$r$ doit augmenter afin de rétablir l’équilibre, déplaçant la courbe IS vers le haut.

De manière équivalente, nous pouvons analyser comment $Y$ change quand $G$ augmente pour un niveau $r$ fixe. Dans ce cas, la partie gauche $Y$ doit augmenter mais, en faisant ça, la partie droite augmente aussi (car $Y$ apparaît dans la fonction de consommation).

$\uparrow Y = \uparrow C(Y,T) + I(r) + \uparrow\bar{G}$

La conclusion est la même: si $G$ augmente, la courbe IS se déplace vers la droite, c’est-à-dire, pour chaque niveau $r$ la valeur $Y$ augmente.

Finalement, nous pouvons calculer exactement l’augmentation nécessaire grâce au multiplicateur. En effet, $\frac{\mathrm{d}Y}{\mathrm{d}G}$ indique de combien $Y$ change quand $G$ change. Nous avons déjà vu que $\frac{\mathrm{d}Y}{\mathrm{d}G} = \frac{1}{1-c_1} > 1$

Par exemple, imaginons que l’économie soit décrite avec les fonctions: \begin{align} C(Y-T) = c_0 + c_1(Y-T) = 4 + 0.6(Y-2) \\\ I(r) = \frac{4}{r} \\\ Y = C(Y-T) + I(r) + G \end{align}

Ainsi, supposons que l’on fixe le taux d’intérêt $r=0.4$ et que les dépenses initiales du gouvernement soient $G=8$ avec un niveau d’imposition $T=2.$ À ce niveau, la valeur de $Y$ est $Y = 52$. Le multiplicateur de $G$ est $\frac{1}{1-c_1}=\frac{1}{1-0.6}=2.5$ Ainsi, si les dépenses publiques augmentent de 1 (donc $\Delta G=1$), le niveau de revenu augmente de $2.5$. Dans notre cas, il passe de $Y=52$ à $Y=54.5$ (faites le calcul!), soit une augmentation de $2.5 \Delta G.$

Augmentation de $T$

Si, au contraire, le gouvernement augmente les impôts $T$, la courbe IS se déplace aussi. Pour le voir, admettons que nous fixons un taux d’intérêt $r$ et analysons comment la courbe doit changer pour garder l’identité $Y = C(Y-T) + I(r) + \bar{G}.$

Si les impôts augmentent, cela veut dire que la consommation diminue, car $C(Y-T) = c_0 + c_1(Y-T)$. Ainsi, suit au changement nous avons: $Y = \downarrow C(Y-\uparrow T) + I(r) + \bar{G}.$

Pour rétablir l’égalité, le côte gauche doit diminuer (ce qui va provoquer un effet en chaîne, car la réduction à gauche induit une nouvelle réduction à droite.) $\downarrow Y = \downarrow C(\downarrow Y-\uparrow T) + I(r) + \bar{G}.$

Par conséquent, quand les impôts augmentent, la courbe IS se déplace vers la gauche. Ce résultat a du sense du point de vue économique: avec plus d’impôts, la consommation est plus faible et, donc, pour n’importe quel taux d’intérêt, le PIB doit être aussi plus faible.

De manière alternative, nous pouvons fixer $Y$ et analyser comment $r$ doit s’ajuster pour rétablir l’équilibre. $Y = \downarrow C(Y-\uparrow T) + I(r) + \bar{G}.$

Comme la partie droite vient de diminuer, il faut que $I(r)$ augmente et, pour cela, $r$ doit diminuer. $Y = \downarrow C(Y-\uparrow T) + \uparrow I(\downarrow r) + \bar{G}.$ Conséquence: la courbe IS se déplace vers le bas.

Enfin, nous pouvons aussi utiliser le multiplicateur pour étuder l’effet. Nous aurons que $\frac{\mathrm{d}Y}{\mathrm{d}T} = -\frac{c_1}{1-c_1}$ Par conséquent, une augmentation de $T$ fait bouger la courbe IS vers la gauche de $\frac{c_1}{1-c_1}.$

Par exemple, imaginons que l’économie soit décrite avec les mêmes fonctions qu’avant: \begin{align} C(Y-T) = c_0 + c_1(Y-T) = 4 + 0.6(Y-2) \\\ I(r) = \frac{4}{r} \\\ Y = C(Y-T) + I(r) + G \end{align}

Ainsi, supposons que l’on fixe le taux d’intérêt $r=0.4$ et que les dépenses initiales du gouvernement soient $G=8$ avec un niveau d’imposition $T=2.$ À ce niveau, la valeur de $Y$ est $Y = 52$. Le multiplicateur de $T$ est $-\frac{c_1}{1-c_1}=-\frac{c_1}{1-0.6}=-1.5$ Ainsi, si les impôts augmentent de 1 (donc $\Delta T=1$), le niveau de revenu diminue de $1.5$. Dans notre cas, il passe de $Y=52$ à $Y=50.5$ (faites le calcul!), soit une réduction de $1.5 \Delta T.$

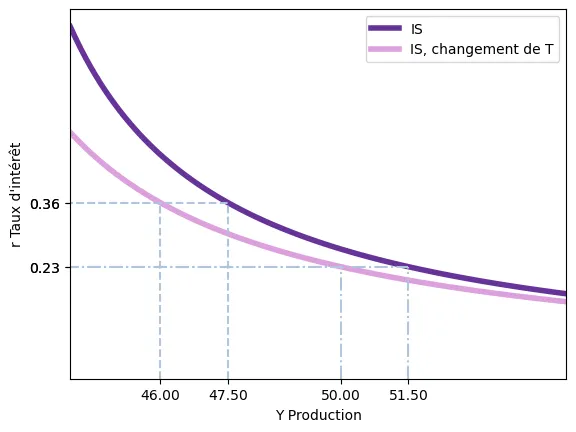
Par exemple, imaginons que $r=0.4,G=8$ et $T$ passe de $T_0 = 3$ à $T_1 = 4$ et que $C(Y-T) = 4 + 0.6(Y-T)$, donc $c_0 = 4$ et $c_1 = 0.6$. Le multiplicateur des impôts est $-\frac{0.6}{1-0.6}=1.5$. La valeur d’équilibre de $Y_0$ est $Y_0 = 47.75$ à $Y_1 = 45.25$, une diminution de $1.5$, qui correspond bien à $- 1.5 \times \Delta T = - 1.5 \times 1$.

Comparaison des multiplicateurs

Nous avons vu précédemment que le multiplicateur des dépenses publiques est $\frac{1}{1-c_1}$, tandis que le multiplicateur des impôts est $-\frac{c_1}{1-c1}$. Il est important de comparer ces deux multiplicateurs pour comprendre leurs implications économiques.

Différence mathématique

En valeur absolue, le multiplicateur des dépenses publiques est toujours plus grand que celui des impôts. En effet, $\left|\frac{1}{1-c_1}\right| > \left|-\frac{c_1}{1-c_1}\right|.$ Cela est vrai car $0 < c_1 < 1$, ce qui implique que $1 > c_1$.

Interprétation économique :

Cette différence mathématique a des implications économiques importantes. Nous pouvons l’expliquer principalement par :

1. Effet direct vs indirect : Une augmentation des dépenses publiques ($\Delta G$) a un effet direct sur le PIB. Chaque euro dépensé par le gouvernement augmente directement le PIB d’un euro. En revanche, une réduction d’impôts ($-\Delta T$) n’a qu’un effet indirect. Elle augmente le revenu disponible, mais seule une fraction de ce revenu supplémentaire, déterminée par $c_1$ (la propension marginale à consommer), est effectivement dépensée.
2. Processus multiplicateur : Pour $\Delta G$, le processus multiplicateur commence immédiatement avec l’intégralité de la dépense. Tout l’argent injecté entre directement dans le circuit économique. Pour $-\Delta T$, seule une partie ($c_1$) de la réduction d’impôts entre dans le circuit économique au début du processus multiplicateur.

Cette différence a des implications importantes pour la politique budgétaire :

• Efficacité : À court terme, une augmentation des dépenses publiques est plus efficace pour stimuler l’économie qu’une réduction d’impôts du même montant.
• Rapidité : L’effet des dépenses publiques se fait sentir plus rapidement car il n’y a pas de délai lié à la décision des ménages de dépenser ou d’épargner.
• Ciblage : Les dépenses publiques peuvent être plus facilement ciblées vers des secteurs ou des projets spécifiques, tandis que l’effet d’une réduction d’impôts dépend des décisions de consommation des ménages.
• Considérations de long terme : Bien que les dépenses publiques aient un effet multiplicateur plus important à court terme, les réductions d’impôts peuvent avoir des effets bénéfiques à long terme sur l’incitation au travail et à l’investissement.

La courbe LM

La deuxième courbe qu’intervient dans le modèle IS-LM est la courbe LM. Cette courbe représente l’équilibre dans le marché de la monnaie, comme dans le modèle classique. En effet, l’économie Keynésienne modifie à peine la demande de monnaie classique.

Le point de départ est le même: on constate que l’offre d’encaisses réeles est éffectuée de manière exogène par la banque centrale. Ainsi, $\frac{M^s}{p}$ représente la quantité d’encaisses réelles offertes par la banque centrale.

Keynes modélise la demande d’encaisses réeles à partir de la préférence pour la liquidité. Selon lui, le taux d’intérêt s’ajuste pour égaliser l’offre et la demande d’encaisses réelles. Il est important de noter que, dans le modèle classique, le taux d’intérêt n’apparaissait pas dans le marché de la monnaie, il se déterminait uniquement sur le marché de l’emprunt.

La demande de monnaie dépend de:

1. Le nombre de transactions à financer (comme dans le modèle classique) L’argent sert comme moyen de transaction. Pour un plus grand nombre de transactions, la demande d’encaisses réelles augmente. Comme le nombre total de transaction est liée au PIB, la demande d’encaisses réelles augmente avec $Y$.
2. Le taux d’intérêt³. Au lieu de détenir de l’argent, les individus peuvent le placer dans un compte pour en obtenir un rendement. En effet, le rendement est le coût d’opportunité de détenir de l’argent. Ainsi, si le taux d’intérêt augmente, les individus préfèrent placer l’argent pour obtenir un revenu issu des taux d’intérêt plus élevé et, donc, la demande d’encaisses réelles diminue avec le taux d’intérêt.

Si nous notons la demande d’encaisses réels par une fonction $L(Y,r)$, nous avons que: \begin{align} \frac{\partial L(Y,r)}{\partial Y} &> 0 \\ \phantom{e} \\ \frac{\partial L(Y,r)}{\partial r} &< 0 \end{align}

Enfin, comme l’offre d’encaisses doit être égale à la demande, la courbe LM est donnée par:

$$\frac{M^s}{p} = L(Y,r)$$

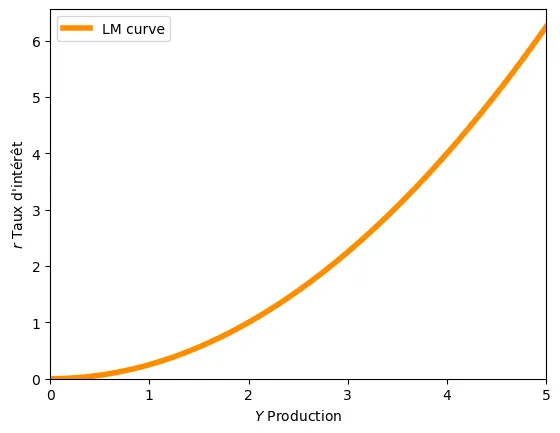
Sur le plan $(Y,r)$, la courbe LM est croissante. Imaginons que $Y$ augmente, ce qui fait que la partie droite de l’équation augmente.

$$\frac{M^s}{p} = \uparrow L(\uparrow Y,r)$$

Pour rétablir l’égalité, il faut diminuer la partie droite (car ni l’offre de monnaie ni le niveau de prix ne changent). Par conséquent, il est nécessaire que $r$ augmente pour faire diminuer la demande. Ainsi, si $Y$ augmente $r$ augmente. Graphiquement:

Déplacement de la courbe LM

De manière similaire à la courbe IS, la courbe LM décrit la relation entre $Y$ et $r$ pour une valeur donnée de $\frac{M^s}{p}.$

Si l’offre d’encaisses réelles varie, la courbe LM se déplace. Imaginons que la banque centrale augmente l’offre d’encaisses réelles. Comme précédemment, nous pouvons analyser l’effet de ce changement en gardant soit $Y$ soit $r$ fixe. Commençons par maintenir $r$ fixe. Avec une augmentation de l’offre d’encaisses réelles, il existe plus d’argent en circulation que ce qu’il faut pour financer le nombre de transactions. Comme le niveau de prix ne peux pas se modifier, la seule possibilité est que le nombre de transactions augmente et, ainsi, que $Y$ augmente. Autrement dit, d’un jour à l’autre, les individus se retrouvent avec plus d’argent dans leurs poches. Ils augmentent leur demande de biens et services, ce qui fait augmenter le PIB.

À l’inverse, si nous fixons maintenant $r$, avec une expansion de l’offre monétaire les agents disposent de plus d’argent que nécessaire. Ainsi, ils vont essayer de le placer dans la banque pour en obtenir des revenus avec le taux d’intérêt, ce qui fait diminuer le taux d’intérêt.

Enfin, mathématiquement: \begin{align} \frac{M^s}{p} &= L(Y,r) \implies \\ \mathrm{d}\frac{M^s}{p} &= L^\prime_Y \mathrm{d}Y \\ \frac{\mathrm{d}Y}{\mathrm{d} \frac{M^s}{p}} &= \frac{1}{L^\prime_Y} > 0 \end{align}

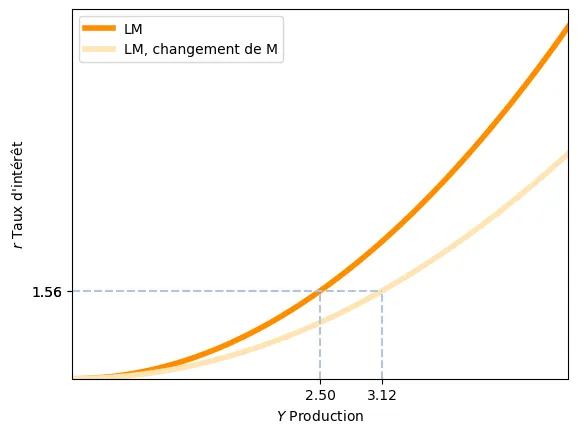
La dernière ligne vient du fait que nous avions montré que $\frac{\partial L(Y,r)}{\partial Y} > 0.$ Ainsi, si l’offre d’encaisses réelles augmente, la courbe LM se déplace vers la droite.⁴

IS-LM

Avec les courbes IS-LM, le modèle est complet. Les deux équations qui déterminent l’équilibre sont:

\begin{align} Y &= C(Y-T) + I(r) + G \tag*{IS} \\ \frac{M^s}{p} &= L(Y,r) \tag*{LM} \end{align}

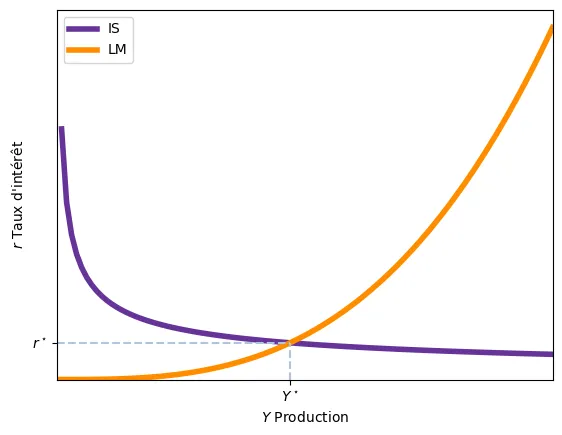
Le modèle prends les variables $T,, G$ et $\frac{M^s}{p}$ comme exogènes. Chaque fois qu’une de ces variables change, un des deux courbes se déplace. Étant donné ces variables exogènes, la courbe IS montre les combinaisons de $r$ (taux d’intérêt) et $Y$ (revenu) qui satisfont l’équation représentant le marché des biens, tandis que la courbe LM fournit les combinaisons de $r$ et $Y$ qui satisfont l’équation représentant le marché monétaire.

L’équilibre de l’économie se situe au point d’intersection des courbes IS et LM. Ce point donne le taux d’intérêt $r$ et le niveau de revenu $Y$ qui satisfont simultanément les conditions d’équilibre sur le marché des biens et sur le marché monétaire.

Le chômage

Pour finir, dans le modèle IS-LM nous pouvons voir le chômage comme une variable qui est déterminée par l’équilibre IS-LM. Vu que $G,, T$ et $\frac{M^s}{p}$ le niveau de revenu (et donc, de production) est fixée, nous pouvons trouver le nombre de travailleurs à l’aide de la fonction de production: $Y=F(\bar{K},N)$ où $Y$ et $\bar{K}$ sont connus. Il est donc clair que le nombre de travailleurs $N$ ne dépend plus des choix des ménages (entre travail et loisir) mais seulement du niveau d’activité économique. Enfin, le salaire d’équilibre assure que le nombre de travailleurs soit celui qui correspond au niveau d’activité d’équilibre.

Exercises

Problem Set 2: IS-LM