Introduction

L’intersection de la courbe IS et de la courbe LM détermine le niveau du revenu national. Lorsque l’une de ces courbes se déplace, l’équilibre à court terme de l’économie change, et le revenu national fluctue. Dans cette section, nous examinerons comment les changements de politique et les chocs économiques peuvent provoquer le déplacement de ces courbes.

Politique budgétaire

Changement de $G$

Imaginons que le gouvernement augmente ses dépenses publiques de $\Delta G$. Cette augmentation aura un effet immédiat et pour un niveau de taux d’intérêt donnée augmente le revenu de $\frac{\mathrm{dY}}{\mathrm{d}G} = \frac{1}{1-_c1} \Delta G$ (le multiplicateur des dépenses). Autrement dit, la courbe IS se déplace vers la droite de $\frac{1}{1-c_1}\Delta G$. Le schéma suivant le montre pour le cas $c_1 = 0.6 \implies \frac{\mathrm{d}Y}{\mathrm{d}G} = \frac{1}{1-0.6}=2.5$ et un niveau $\Delta G = 10$.

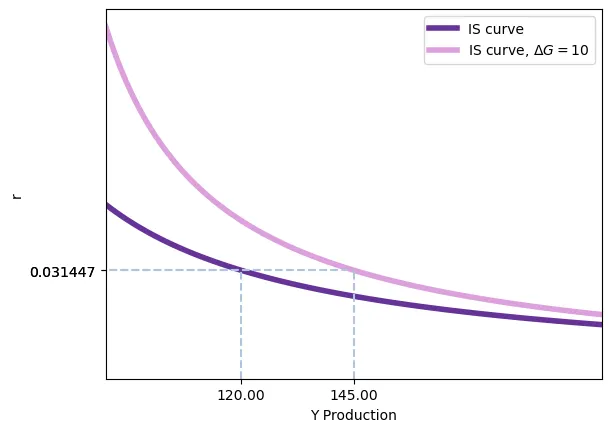
Comme on le voit, pour le taux d’intérêt $r \approx 0.031$, le niveau de revenu passe de $Y=120$ à $Y=145$, soit une augmentation de $25$ qui correspond à $\frac{1}{1-c_1} \Delta G= 2.5 \times 10 = 25$.

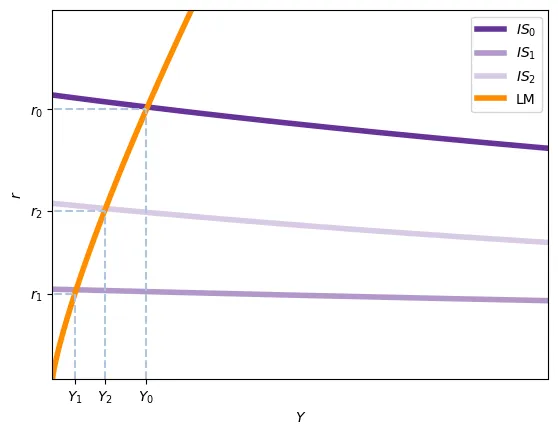
Or, en équilibre, le revenu n’augmentera pas autant car une partie de cette hausse se transforme en une augmentation du taux d’intérêt d’équilibre. On peu le voir sur le schéma suivant où nous indiquons le niveau $Y = 145$ comme référence. Il est évident que l’augmentation de $G$ augmente $Y$ et $r$.

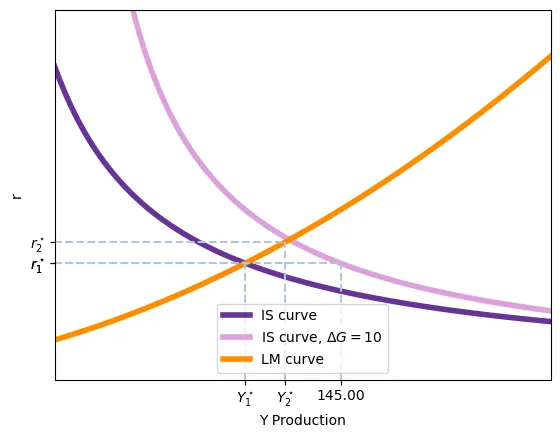
Pour quoi on ne voit pas une augmentation de $Y$ égale à $\frac{\mathrm{d}Y}{\mathrm{d}G} \Delta G= \frac{1}{1-c_1}\Delta G$?

La réponse se trouve dans la courbe LM. Imaginons le cas suivant: quand le gouvernement augmente $G$, cela implique une hausse de $Y = \frac{1}{1-c_1}\Delta G$. Mais, la banque centrale n’a pas modifié sa politique monétaire et les encaisses réels en circulation sont constants. Ainsi, au marché de la monnaie, la demande de monnaie augmente (car $L(Y,r)$ augmente avec $Y$) mais l’offre n’a pas changé. Pour se ré-équilibrer, il est nécessaire que la demande diminue, et cela implique une hausse de $r$. Or, l’augmentation de $r$ a ses répercussions sur le marché des biens car elle rend l’investissement plus couteaux et les entreprises décident d’investir moins car $I(r)$ diminue avec $r$. En conséquence, le niveau de revenu diminue, réduissant en partie l’effet expansionniste des dépenses publiques.

En résumé, le déplacement horizontal de la courbe IS est égal à l’effet multiplicateur. Ceci est plus grand que la hausse total du revenu en équilibre car l’augmentation des dépenses publiques ont un effet d’éviction sur l’investissement qui augmente le taux d’intérêt.

Le multiplicateur total de $G$

Nous pouvons nous demander s’il est possible de calculer l’effet total d’une augmentation de $G$ sur $Y$ en considérant l’effet d’éviction. Ceci est possible avec quelques dérivées: Le point de départ est l’équilibre définit par le modèle IS-LM: \begin{align} Y &= c_0 + c_1 (Y-T) + I(r) + G \\ \frac{M^s}{p} &= L(Y,r) \end{align}

Quand $G$ change, cela provoque des changements dans $Y$ et $r$ qu’il faut considérer.¹ \begin{align} \mathrm{d} Y &= c_1 \mathrm{d} Y + I^\prime \mathrm{d} r + \mathrm{d}G \\ 0 &= L^\prime_Y \mathrm{d}Y + L^\prime_r \mathrm{d}r \end{align}

Ainsi $0 = L^\prime_Y \mathrm{d}Y + L^\prime_r \mathrm{d}r \implies \mathrm{d}r = - \frac{\overbrace{L^\prime_Y}^{>0} \mathrm{d}Y}{\underbrace{L^\prime_r}_{<0}}$. On peu le remplacer dans la première équation: \begin{align} \mathrm{d} Y &= c_1 \mathrm{d} Y + I^\prime \textcolor{red}{\mathrm{d} r} + \mathrm{d}G \\ \mathrm{d} Y &= c_1 \mathrm{d} Y + I^\prime \textcolor{red}{(-1)\frac{L^\prime_Y \mathrm{d}Y}{L^\prime_r}} + \mathrm{d} G \\ (1-c_1+I^\prime \frac{L^\prime_Y}{L^\prime_r})\mathrm{d}Y &= \mathrm{d}G \\ \frac{\mathrm{d}Y}{\mathrm{d}G} &= \frac{1}{1-c_1+\textcolor{green}{I^\prime \frac{L^\prime_Y}{L^\prime_r}}} \end{align}

Le terme en vert représente l’effet d’éviction.

Cette analyse nous permet d’examiner les conditions sous lesquelles l’effet multiplicateur d’une augmentation des dépenses publiques ($G$) sur le revenu national ($Y$) sera plus important. En tenant compte de l’effet d’éviction calculé précédemment, nous pouvons identifier les facteurs qui influencent l’ampleur de la transmission de la hausse de $G$ à $Y$. Quelques points à considérer pour approfondir cette réflexion :

1. La sensibilité de l’investissement au taux d’intérêt: L’effet d’éviction est dû au fait que l’augmentation de la demande d’encaisses implique une hausse de $r$. Si l’investissement se réduit beaucoup quand $r$ augmente, l’effet d’éviction sera plus important ($I^\prime \rightarrow 0$) Ceci est représenté par le terme $I^\prime$ qui mesure la sensibilité de $I$ aux changements de $r$. Dans la cas extrême où l’investissement est constante, $I^\prime = 0$ et l’effet d’éviction est zéro. Dans ce dernier cas, la courbe IS est verticale.

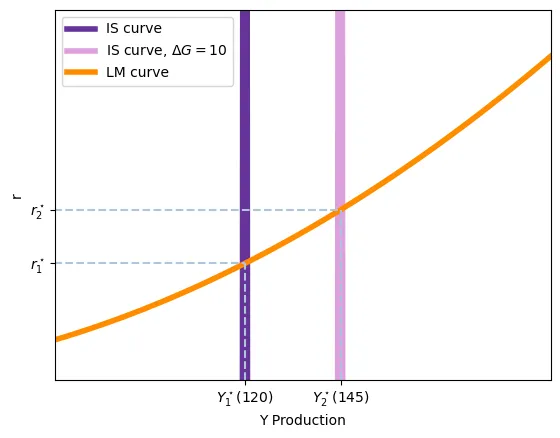
2. La demande d’encaisses réels ne dépend pas du niveau de revenu: La hausse du type d’intérêt vient du fait qu’avec l’augmentation du revenu induite par $\Delta G$, la demande d’encaisses réels augmente. Si la demande d’encaisses réels ne change pas avec le revenu, l’effet d’éviction devient zéro. ($L^\prime_Y \rightarrow 0$). Ceci est, néanmoins, très improbable car les encaisses servent à financer les transactions. Dans ce cas-là, la courbe LM serait horizontale.

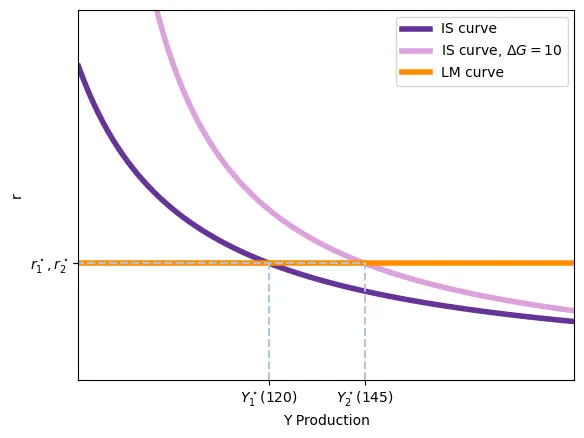
3. La demande d’encaisses réels est très sensible aux changements de $r$: De manière similaire au cas dernier, si la demande d’encaisses est très sensible aux changements du taux d’intérêt, l’effet d’éviction se minimise. Dans ce cas, une petite augmentation en $r$ entraînerait une réduction très importante des encaisses réels. ($L^\prime_r \rightarrow \infty$). Par conséquent, il serait possible de compenser l’augmentation de la demande de monnaie induite par $\Delta G$ avec une augmentation infinitésimale de $r$ qui ne ferait varier pas l’investissement. Si la demande d’encaisses réels est très réactive par rapport à $r$, la courbe LM devient horizontale.

Changement de $T$

Un deuxième outil à disposition du gouvernement est le niveau des impôts. Les implications d’un changement dans $T$ sont les mêmes que pour les changements de $G$, exception faite que les impôts affectent le revenu disponible et, par conséquence, la consommation. En plus, comme nous le savons déjà, un changement en $T$ implique un multiplicateur ($-\frac{c_1}{1-c_1}$) moins important qu’un changement en $G$ de la même ampleur. Ainsi, une réduction des impôts déplace la courbe IS vers la droite et, en équilibre, augmente le niveau de revenu et le taux d’intérêt. Le schéma suivant le montre pour le cas $c_1 = 0.6 \implies \frac{\mathrm{d}Y}{\mathrm{d}T} = \frac{0.6}{1-0.6}=1.5$ et un niveau $\Delta T = -10$. Note: pour comparaison, le schéma est tracez avec une réduction de $T$ de 10, égale à $\Delta G$ auparavant pour faciliter la comparaison.

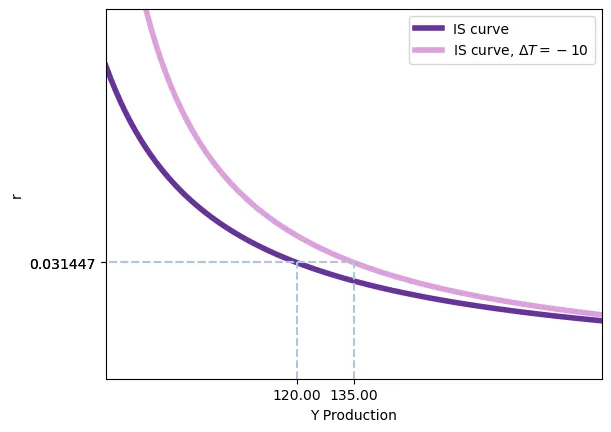
On voit que, pour un même changement (10), le déplacement que la courbe IS connaît est inférieur. Néanmoins, de manière analogue au cas d’une augmentation de $G$, l’effet total sur $Y$ n’est pas égal à $\frac{c_1}{1-c_1}$ car l’augmentation du revenu causée par $-\Delta T$ a comme effet une hausse de la demande d’encaisses réels, qui augmente le taux d’intérêt et réduit ensuite l’investissement.

Le multiplicateur total de $T$

Il est possible de montrer que le multiplicateur total de $T$, une fois considéré l’augmentation du taux d’intérêt est:

$$\frac{\mathrm{d}Y}{\mathrm{d}T} = -1 \times \frac{c_1}{1-c_1+I^\prime \frac{L^\prime_Y}{L^\prime_r}}$$

Politique monétaire

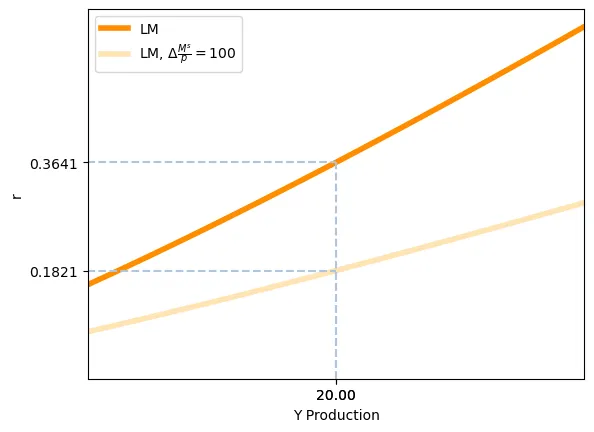
Imaginons que la banque centrale augmente la masse monétaire de $\Delta M$. Cette augmentation aura un effet immédiat sur le marché monétaire: maintenant, il y a plus de monnaie en circulation que la quantité souhaité par les individus. Une correction se met en place immédiatement: et pour un niveau de revenu donné, le taux d’intérêt diminue pour décourager les individus de placer leur argent auprès de la banque. La réduction de $r$ implique ainsi que les individus voudront détenir plus de monnaie, car l’usage alternatif (le placer à la banque) est moins attractive. En conséquence, quand $\frac{M^s}{p}$ augmente $r$ diminue pour un niveau $Y$ donné. Sur le plan $(Y,r)$ cela est équivalent à dire que la courbe LM se déplace vers la droite.

Cette diminution du taux d'intérêt encourage l'investissement, ce qui augmente le revenu car $Y = C(Y-T) + I(r) + G$. Enfin, cette hausse de $Y$ fait augmenter la demande d'encaisses réels, ce qui fait réduire le taux d'intérêt; et le cycle continue jusqu'à atteindre l'équilibre.

Par conséquence, comme dans le cas de la politique budgétaire, la réduction du taux d’intérêt n’est pas celui impliqué par le multiplicateur et une partie se retrouve comme augmentation du revenu $Y$.

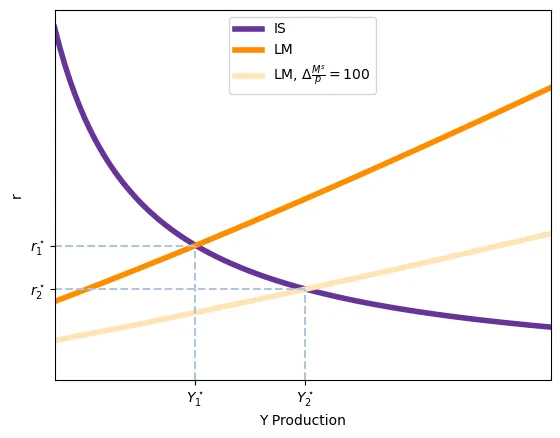
Trappe de liquidité

Le potentiel de la politique monétaire pour redresser une situation de crise économique se basse essentiellement sur sa capacité de réduire le taux d’intérêt pour augmenter le niveau d’investissement. Mais, que se passe-t-il quand le taux d’intérêt est déjà zéro?

Par exemple, aux USA pendant la Grande Récession le taux d’intérêt était bien dessous de 1%, et pendant la crise de 2008 la Réserve Fédérale diminuait le taux d’intérêt entre 0 et 0.25%.

Cette situation se connaît comme trappe de liquidité. Dans ces cas, une politique monétaire expansionniste est incapable de faire diminuer les intérêt.

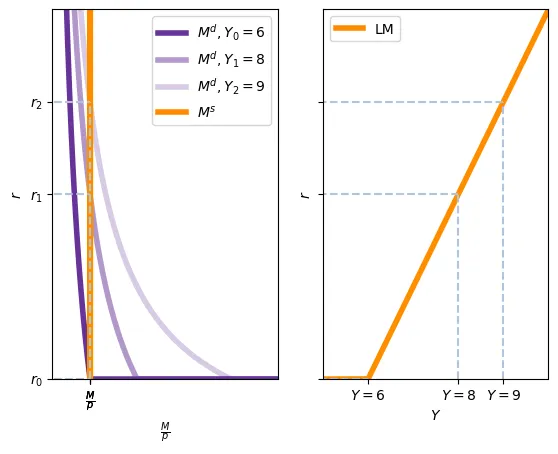
Dans le schéma, les différentes courbes $M^d$ montrent la demande d’encaisses réels pour différents valeurs de $Y$. À mesure que $Y$ diminue (lors d’une crise, par exemple) le taux d’intérêt d’équilibre devient zéro. Alors, une augmentation de la masse monétaire n’aurait aucun effet sur $r$. Imaginez que $Y=6$, si l’on déplace la courbe LM vers la droit suivant une augmentation de $\frac{M^s}{p}$, le taux d’intérêt continuerait à 0.

En d’autres termes : lorsque le taux d’intérêt est égal à zéro, l’économie tombe dans une trappe à liquidité. La banque centrale peut augmenter la liquidité – c’est-à-dire, accroître la masse monétaire. Mais cette liquidité tombe dans une trappe : l’argent supplémentaire est volontiers détenu par les investisseurs financiers à un taux d’intérêt inchangé, à savoir zéro. Si, à ce taux d’intérêt nul, la demande de biens est encore trop faible, alors la politique monétaire ne peut plus rien faire pour augmenter la production.

Le modèle IS-LM dans le monde

La Grande Dépression (1929-1939)

Pendant la Grande Dépression la demande aux USA était très faible à cause de la chute de la bourse (donc, une moindre consommation minimale) et le faible taux d’investissement. Pour y faire face, le président Franklin D. Roosevelt a introduit le New Deal, un ensemble de programmes et de réformes économiques destinés à relancer l’économie américaine. Le New Deal comprenait des projets de travaux publics, des aides sociales, et des réformes financières. Selon le modèle IS-LM, une augmentation des dépenses publiques déplace la courbe IS vers la droite. Cette augmentation des dépenses stimule la demande globale, augmentant ainsi le revenu national et réduisant le chômage.

"The country needs and, unless I mistake its temper, the country demands bold, persistent experimentation. It is common sense to take a method and try it: If it fails, admit it frankly and try another. But above all, try something."

On peut analyser la situation à l’aide du modèle IS-LM. Imaginons que la demande originale, avant la crise, était: $Y = 2 + 0.6(Y-T) + \frac{1}{r} + G$ Avec la crise, les ménages décident de consommer moins et les entreprises investissent aussi moins, ansi la demande devient: $Y = 0.5 + 0.6(Y-T) + \frac{0.5}{r} + G$ Enfin, on imagine que le New Deal augmente les dépenses de $G=4$ à $G_1 = 8$ tout en maintenant le reste de l’économie inchangée. Pour simplifier l’analyse, on pose que ni la l’offre ni la demande d’encaisses réels ne changeaient pas.

Crise en Espagne (2008-2014)

Pendant la crise économique en Espagne de 2008 à 2014, la demande intérieure était très faible en raison de l’éclatement de la bulle immobilière et de la crise financière mondiale, ce qui a entraîné une réduction de la consommation et des investissements.

Pour faire face à cette crise, le président José Luis Rodríguez Zapatero a introduit le Plan-E, un ensemble de mesures économiques destinées à relancer l’économie espagnole. Ce plan visait à stimuler la demande globale par des projets de travaux publics et une augmentation des dépenses publiques. En termes du modèle IS-LM, cette augmentation des dépenses publiques aurait déplacé la courbe IS vers la droite, augmentant ainsi le revenu national et réduisant temporairement le chômage.

El País

Los más de 30.000 proyectos del fondo -conocido simplemente como Plan Zapatero- han traído un chaparrón de dinero a los ayuntamientos: 8.000 millones de euros, cifra que duplica la inversión de todos los municipios de España al año. Y han permitido el nada desdeñable logro de ocupar a más de 410.000 personas y hacer que el desempleo lleve tres meses de caídas en un momento en el que el paro se ha convertido en un drama nacional.

Cependant, lorsque les économies d’Europe ont commencé à se redresser, l’Espagne a dû mettre en place des mesures de contrôle du déficit, ce qui a réduit les dépenses publiques (G) et augmenté les impôts (T). Ces mesures d’austérité ont aggravé la crise en réduisant encore plus la demande globale.

Une autre dimension de la crise espagnole est l’importance du secteur informel, qui s’est accru en raison de la crise. L’augmentation de la demande de monnaie due à l’expansion du secteur informel a déplacé la courbe LM vers le haut, ce qui a empiré la crise en augmentant les taux d’intérêt et en réduisant encore plus l’investissement.

Contrôle de déficit

Pour finir, une situation classique est le contrôle du déficit public. Par exemple, en 2024 la France dépassait le niveau fixé par l’UE en termes de déficit maximal Public Senat

Ce vendredi 26 juillet [2024], la Commission européenne a annoncé placer la France en procédure de déficit excessif, compte tenu du dévissage de la trajectoire des finances publiques. En effet avec une dette publique qui atteint 110 % du PIB et un déficit public réévalué à 5,5 % du PIB à cause d’une surestimation de la croissance, la France ne respecte pas les critères posés par le Pacte de stabilité et de croissance qui demande aux Etats membres de l’Union européenne de ne pas avoir un niveau d’endettement supérieur à 60 % du PIB et de ne pas dépasser un déficit de 3 % du PIB.

Pour rétablir l’équilibre budgétaire, il est nécessaire de réduire $G$ ou augmenter $T$ (ou utiliser les deux simultanément). On peut se demander quel est le meilleur moyen pour attendre l’équilibre de manière à affecter le PIB le moins possible.

Imaginons qu’on peut décrire l’économie française avec les fonctions suivantes et que, initialement, $\frac{M^s}{p}=0.078, T=0.445, G=0.5$. \begin{align} Y &= 0.1 +0.4(Y-T) + 0.1 + \frac{1}{r} + G \\ \frac{M^s}{p} &= \frac{Y}{r} \end{align}

Nous pouvons calculer les valeurs d’équilibre. D’après l’équation pour LM: $$\frac{0.078}{Y} = \frac{1}{r}$$ Ainsi, \begin{align} Y &= 0.1 + 0.4(Y-0.445) + 0.1 + \frac{0.078}{Y} + 0.5 \\ Y^2 &= 0.1 Y + 0.4(Y^2-0.445 Y) + 0.1 Y + 0.078 + 0.5 Y \\ 0 &= -(1-0.4)Y^2 + 0.522 Y + 0.078 \\ Y &= \frac{-0.522-\sqrt{0.522^2+4 \times 0.6 \times 0.078}}{-2(1-0.4)} \\ Y &= 1 \end{align} Par conséquence, le déficit est de $\frac{T-G}{Y} = \frac{0.055}{1} = 0.055$

Comme le multiplicateur total associé aux dépenses publiques $\left(\frac{\mathrm{d}Y}{\mathrm{d}G} = \frac{1}{1-c_1+I^\prime\frac{L^\prime_Y}{L^\prime_r}}\right)$ est plus important que celui associé aux impôts $\left(\frac{\mathrm{d}Y}{\mathrm{d}T} = \frac{c_1}{1-c_1+I^\prime\frac{L^\prime_Y}{L^\prime_r}}\right)$ une réduction d’un euro dans les dépenses publiques pénalise le revenu plus qu’une augmentation des impôts d’une unité. Ainsi, le meilleur que le gouvernement pourrait faire est d’augmenter les impôts jusqu’à ce que le déficit soit de 3%.

Attention, si l’on essaie de dire que $T=0.47$ et que, donc $\frac{G-T}{Y} = \frac{0.5-0.47}{1} = 0.03$ on aurait tort, car avec une augmentation de $T$ le revenu ($Y$) diminue.

Calculons le niveau de revenu comme une fonction des paramétres du modèle:

\begin{align} Y &= c_0 + c_1(Y-T) + i_0 + \frac{1}{r} + G \quad\text{et} \quad \frac{M^s}{p} = \frac{Y}{r} \implies \\ Y &= c_0 + c_1(Y-T)+i_0 + \frac{\frac{M^s}{p}}{Y} + G \\ Y^2 &= c_0 Y + c_1(Y^2-T Y) + \frac{M^s}{p} Y + G Y \\ 0 &= -(1-c_1)Y^2 + (c_0 + c_1 T - G)Y + \frac{M^s}{p} \\ Y^{eq} &= \frac{c_0+G+i_0-c_1 T + \sqrt{4(1-c_1)\frac{M^s}{p}+(c_0+G+i_0+c_1 T)^2}}{2(1-c_1)} \\ Y^{eq} &= \frac{5}{6}\left(0.7+\sqrt{1.872+\left(\frac{2T}{5}-0.7\right)^2}-\frac{2 T}{5}\right) \end{align}

Ainsi, on cherche le niveau $T$ tel que $\frac{0.5-T}{Y^{eq}} = 0.03$

\begin{align} 0.03 &= \frac{0.5-T}{\frac{5}{6}\left(0.7+\sqrt{1.872+\left(\frac{2T}{5}-0.7\right)^2}-\frac{2 T}{5}\right)} \\ T &= 0.478744 \\ Y^{eq} &= 0.980138 \end{align}

Si, par contre on cherchait à réduire les dépenses (parce que les présidentielles approchent), cela impliquerait que le revenu diminue davantage.

Ainsi, \begin{align} Y^{eq} &= \frac{c_0+G+i_0-c_1 T + \sqrt{4(1-c_1)\frac{M^s}{p}+(c_0+G+i_0+c_1 T)^2}}{2(1-c_1)} \\ Y^{eq} &= \frac{5}{6}\left(0.022+\sqrt{0.1872+(G+0.022)^2}+G\right) \end{align}

De manière similaire à avant, on cherche le niveau $G$ tel que $\frac{G-0.445}{Y^{eq}} = 0.03$

\begin{align} 0.03 &= \frac{G-0.445}{\frac{5}{6}\left(0.022+\sqrt{0.1872+(G+0.022)^2}+G\right) } \\ G &= 0.466896 \\ Y^{eq} &= 0.951459 \end{align}

Exercises

Problem Set 3: IS-LM, part 2