2 Introduction

Le cours de Macroéconomie dynamique porte sur le sujet de la croissance économique à long terme. Cela représente une différence majeure par rapport au modèle IS-LM que vous avez déjà étudié, car ce dernier se concentre sur les fluctuations économiques à court terme.

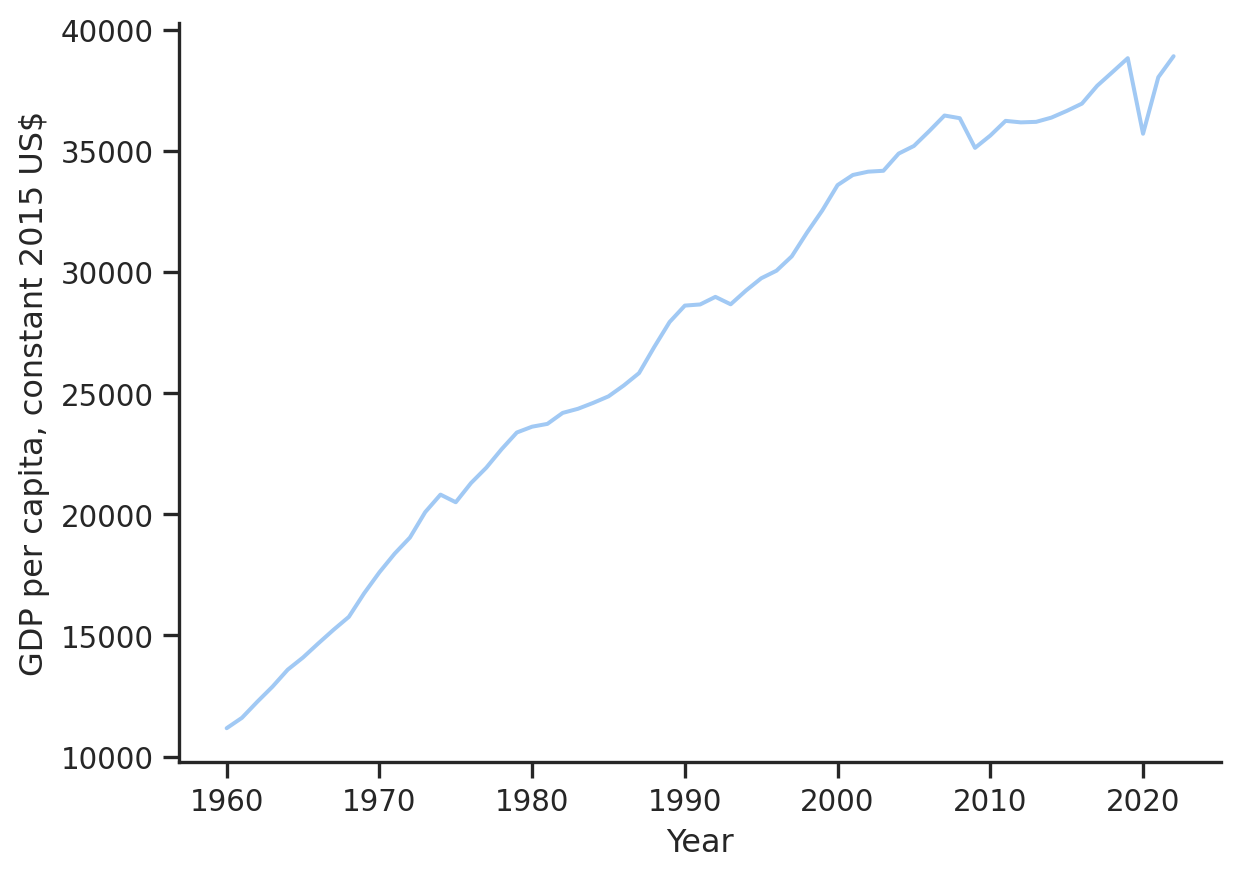
Pour illustrer les limites du modèle IS-LM, examinons la Figure 2.1 représentant l’évolution du PIB par habitant en France.

Figure 2.1: Évolution du PIB par habitant en France (en dollars constants de 2015)

Selon le modèle IS-LM, le PIB peut augmenter en raison de changements qui déplacent soit la courbe IS, soit la courbe LM. Par exemple, une politique budgétaire qui augmente les dépenses publiques ou une politique monétaire qui augmente la base monétaire. Cependant, il est difficile de croire que le gouvernement augmentera continuellement l’un ou l’autre de ces facteurs¹. Il est donc nécessaire de chercher ailleurs pour comprendre pourquoi nous observons une croissance économique.

En effet, une compréhension des déterminants de la croissance économique devient fondamentale si nous voulons étudier les écarts de revenus entre les pays, car les effets de la croissance s’accumulent rapidement. Par exemple, entre 1870 et 2000, le PIB par habitant des États-Unis est passé de 3 340$ à 33 330$. Supposons pour un instant que le taux de croissance ait été constant pendant ces 130 années et calculons-le.

\[ PIB_{2000} = PIB_{1870} \times e^{(g(2000-1870))} \]

où $g$ est le taux de croissance. Cela nous donne $g \approx 0.018$, soit une croissance moyenne de 1,8%. En revanche, avec un taux de croissance légèrement plus faible, de 0,8% (soit 1% de moins), le PIB par habitant aujourd’hui ne serait que de $PIB_{2000} = PIB_{1870} \times e^{(0,008(2000-1870))} = 9 450$. Ainsi, au lieu d’être la deuxième économie en 2020, elle serait classée 45e, au même niveau que le Mexique ou la Pologne.

Les modèles macroéconomiques dynamiques nous fournissent des outils pour étudier les déterminants de la croissance économique. Par exemple, pourquoi Hong Kong a-t-elle enregistré un taux de croissance annuel de 5,4 % entre 1960 et 2000, différent de celui des États-Unis ? Les théories de la croissance économique nous permettent également d’aborder la question de la convergence : est-ce que les pays les plus pauvres peuvent avoir des taux de croissance plus élevés que ceux des pays développés et les rattraper ? Ou est-ce que l’écart se creusera davantage ? Les pays similaires ont-ils tendance à converger vers un même niveau de PIB par habitant ?

Le cours est basé sur Barro et Sala-i-Martín (2004) et Romer (2019).

2.1 Croissance économique

Les théories modernes de la croissance économique, basées sur l’approche néoclassique, comprennent plusieurs éléments essentiels :

Concurrence
Rendements décroissants
Accumulation de capital (physique et humain)
Progrès technologique

D’un point de vue historique, nous pouvons commencer par le modèle de Solow (1956). Ce modèle propose une fonction de production à rendements constants, des rendements décroissants pour chaque facteur et un taux d’épargne constant. Le modèle de Solow sert de base à de nombreux autres modèles et est utilisé comme point de référence. Selon ce modèle, les pays les plus pauvres ont un taux de croissance plus élevé que les pays les plus riches, et les pays similaires atteignent des niveaux de croissance similaires (convergence conditionnelle). Cependant, le modèle présente un problème : en l’absence de source de croissance technologique, il prédit un taux de croissance à long terme de 0 pour le PIB par habitant. Étant donné que nous avons observé des taux de croissance positifs pendant plus d’un siècle, des extensions ont été proposées pour résoudre ce problème.

La première extension suppose simplement une augmentation exogène de la technologie. Dans ce cas, le PIB par habitant peut continuer à augmenter. Cependant, cela ne nous aide pas à comprendre pourquoi les pays sont différents, car cela revient à dire que leur taux de croissance technologique est différent.

Le modèle Ramsey-Cass-Koopmans (1965) modifie le modèle de Solow en permettant aux ménages de décider de manière optimale combien épargner. Dans le modèle de Solow, le taux d’épargne était exogène. Cette modification rend le modèle plus complexe et enrichit les dynamiques, mais les conclusions restent les mêmes.

D’autres modèles tentent de modéliser la croissance technologique de manière plus explicite. Par exemple, Arrow (1962) et Romer (1986) proposent des modèles où les connaissances sont acquises par le biais de la production (apprentissage par la pratique). Du point de vue théorique, cela revient à considérer la croissance technologique comme une externalité de la production. Plus tard, Romer (1987, 1990) ajoute un secteur de l’économie dédié à la création d’idées et introduit la concurrence imparfaite pour protéger les idées. Une autre approche pour modéliser la création de nouvelles idées est le paradigme schumpétérien, où les individus inventent des nouvelles technologies qui surpassent les précédentes, par exemple Aghion et Howitt (1992).

2.2 Échantillon d’Annales

Exemple des questions posées lors des années précédentes

On suppose une économie comme celle décrite dans le modèle de Solow :
- Un seul bien homogène existe.
- De nombreuses entreprises homogènes produisent ce bien avec une fonction de production Cobb-Douglas.
- La production nécessite du capital $K$ et du travail $L$.
- La concurrence est pure et parfaite, et les facteurs de production sont rémunérés à leur productivité marginale.
- Des ménages homogènes épargnent une faction constante $s$ de leur revenu.
- La population augmente au taux constant et exogène $n > 0.$
- Le temps $t$ est continu.
Ainsi, au moment $t$, la production totale est $Y(t) = K(t)^\alpha L(t)^{1-\alpha}$.
1. Si l’on denote le capital par tête comme $k(t) \equiv \frac{K(t)}{L(t)}$ et la production par tête comme $y(t) = \frac{Y(t)}{L{t}}$, écrivez la fonction de production en termes intensifs, c’est-à-dire, trouvez une équation $y = f(k).$
2. Calculez le salaire et le taux d’intérêt.
3. Dans cette économie, le capital physique s’accumule selon l’équation dynamique $\dot{K}(t) = s Y(t) - \delta K(t)$ où $\delta \in (0,1)$ est le taux de dépréciation du capital. Déduisez l’équation d’accumulation du capital par tête, c’est-à-dire, l’équation pour $\dot{k}(t)$.
4. Définissez, avec vos propres mots, le concept d’état stationnaire, et calculez tous les états stationnaires qui existent pour cette économie.
5. Décrivez les dynamiques de l’économie, c’est-à-dire, expliquez comment le capital par tête évolue avec le temps. Vous pouvez vous aider d’un graphique ou faire référence à l’idée de stabilité des états stationnaires.
Dans le modèle de Ramsey, les deux équations dynamiques qui expliquent l’évolution de l’économie sont : \[\begin{align*} \frac{\dot{c}(t)}{c(t)} &= \frac{1}{\theta}\left(f^\prime(k(t)) - \rho - \delta \right) \\ \dot{k}(t) &= f(k) - c(t) - (n + \delta) k(t) \end{align*}\]
1. Expliquez pour quoi la consommation
  - augmente avec l’élasticité de substitution intertemporelle $\left(\frac{1}{\theta}\right).$
  - diminue avec la valuer de $\rho$ (bias pour le présent, aidez-vous de la fonction d’utilité pour en discuter)
2. Tracez le diagramme de phase qui correspond à l’économie.
  1. À partir de l’équation dynamique pour le capital, montrez l’ensemble de points où $\dot{k}(t) = 0$ et expliquez les dynamiques du capital lorsque la consommation n’assure pas $\dot{k}(t) = 0$, c’est-à-dire, lorsque $c$ est plus grand (ou plus petite) que la valeur qui assure $\dot{k}(t) = 0.$
  2. À partir de l’équation dynamique pour la consommation, montrez l’ensemble de points où $\dot{c}(t) = 0$ et expliquez les dynamiques de la cosommation lorsque le capital n’assure pas $\dot{c}(t) = 0$, c’est-à-dire, lorsque $k$ est plus grand (ou plus petite) que la valeur qui assure $\dot{c}(t) = 0.$
  3. Combinez les dynamiques du capital et de la consommation pour illustrer les différentes dynamiques globales qui peuvent exister dans le modèle de Ramsey, et indiquez au moins une possible évolution du capital et de la consommation qui amène vers l’état stationnaire.
Dans le contexte du modèle de Solow, veuillez expliquer la règle d’or. On distingue deux cas différents selon que le niveau stationnaire du capital ($\bar{k}$) est plus élevé ou plus bas que celui correspondant à la règle d’or ($k_\text{gold}$): situation d’ineficacité dynamique et situation d’éfficacité dynamique.
1. Expliquez comment l’économie peut sortir de la situation d’ineficacité dynamique et atteindre une situation Pareto-optimale.
2. Expliquez pour quoi il n’est pas possible d’introduire une telle politique pour sortir de la situation d’efficacité dynamique.
Dans le modèle de Solow avec une fonction de production Cobb-Douglas, le taux de croissance du capital (par tête) est défini comme suit: $g_k \equiv \frac{\dot{k}(t)}{k(t)} = s k(t)^{\alpha -1} - (n+\delta).$
1. Montrez que ce taux de croissance $g_k$ diminue avec le niveau de capital existant $k(t).$
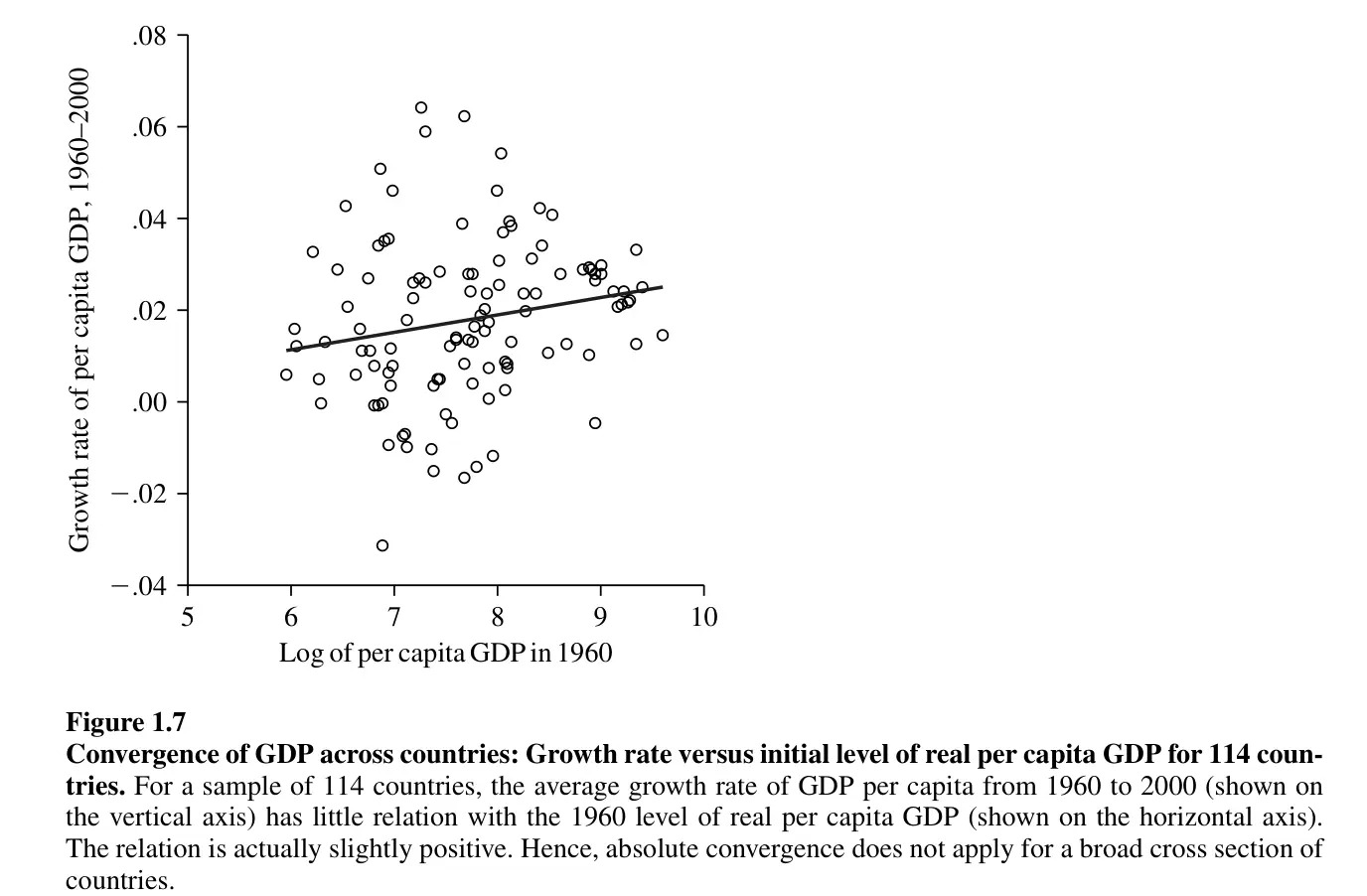
2. Quelles sont les implications en termes de convergence économique entre pays ?
3. Pourquoi une comparaison entre pays, comme celle présentée dans le graphique suivant, ne montre-t-elle pas de convergence ?

De plus, le graphique montre le PIB réel, donc net des effets monétaires.↩︎