Époques dans le modèle unifié de croissance économique

La théorie unifiée de la croissance économique

L’évolution des variables qu’intégrent le modèle générent trois grandes époques selon sa valeur: époque Malthusienne, époque post-Malthusienne et époque moderne. Chacune des époque se caractérise une combinaison particulier des variables (ou des dynamiques des variables) sous-jacentes suivantes:

• Fertilité et sa relation avec le revenu par tête (positive ou negative).
• Investissement dans l’éducation (positive ou zéro).

Enfin, il faut signaler que chaque époque a une durée temporelle différente. Ainsi, l’époque Malthusienne est la plus longue, prenant dès l’apparition des êtres humains modernes jusqu’à le 18è siècle pour les pays développés. Ensuite, l’époque post-Malthusienne prend les siècles 18è et 19è, et à partir de ce point là, on entre dans l’époque moderne. Enfin, avant d’entrer dans le détail, il est nécessaire de décrire le rôle de l’éducation dans le modèle.

Éducation et capital humain dans le modèle unifié de croissance économique

Dans le modèle unifié de croissance économique, les parents investissent dans l’éducation des enfants parce qu’ils attirent de l’utilité de leur niveau de capital humain, et celui-là est fortement influencé par le niveau d’éducation. L’hypothèse que les parents préférent avoir des enfants éduqués est una maniẽre simple et typique de représenter des préférences plus complexes:

• Les parents s’intéressent au futur salaire des enfants, et le salaire augmente avec le niveau éducatif.
• Les parents ont une simple préférence pour l’éducation,

Une nouveauté de la théorie unifiée de la croisance économique est qu’elle introduit la possibilité que le capital humain se déprecie, et la vitesse de la dépréciation est une fonction du niveau technologique (voir en dessous). En plus, on suppose que tous les enfants sont équipés d’un certain niveau de capital humain, même si leurs parents n’investissent pas dans l’éducation. Ces deux hypothèses, innocentes en principe, ont des profondes consequénces sur l’évolution de l’éducation.

Dépreciation du capital humain

La prèmiere hypothèse peut s’expliquer de la manière suivante. Imaginons une société dans laquelle le niveau technologique est faible et ne change pas. Alors, tout ce qu’on apprend pendant la jeunesse (un métier, par exemple) va rester utile tout la vie. Par exemple, si on apprend à utiliser une scie ou un marteu, ces connaissances restent valides autant que les outils ne changent pas. Pour tant, éduquer les enfants n’apporte des avantages, car la technologie va rester la même. Par contre, si maintenant on suppose que la technologie change rapidement, il est possible que les outils de demain ne soient pas une scie et un marteu, mais une scie controlée par ordinateur et un marteau pnéumatique. Dans ce cas-là, les connaisances acquises pendant la jeunesse sont vite dépassées, et pour tant, si on fournie aux enfants de l’éducation ils seront mieux équipés pour s’adapter à la nouvelle situation. Ainsi, les parents doivent procurer à leurs enfants de l’éducation pour amortir la dépréciation du capital humain dû au progrès technique.

Niveau minimal de capital humain

Comment on a dit auparavent, il est raisonable que même sans un investissement exprès en capital humain, un certain niveau est toujours atteint. Par exemple, on apprend certaines choses, y compris des métiers, par la simple observation.

Implications

Les implications de ces hypothèses sont claires: vu que les enfants sont équipés d’un niveau minimum de capital humain, et vu qu’avec un faible progrès technologique l’éducation n’est pas nécéssaire, les investissements en éducation ne deviendran positifs qu’avec le temps. Autrement dit, quand les ressources sont peu abondantes, les parents préférent les affecter à la nourriture et au nombre d’enfants plutôt qu’à l’éducation. Seulement à partir d’un certain niveau de richesse (l’éducation est un bien de luxe dans ce modèle) ou de progrès technologique il y aura des investissements dans l’éducation.

Changement technologique

Pour finir, le modèle postule que la technologie avance grâce à deux effets:

• D’un côté, on suppose que les gens ont, de manière aléatoire, des nouvelles idées qui augmentent le niveau technologique. Ainsi, une population plus large aura une nouvelle idée avec une plus grande probabilité, et pour tant, l’avancement technologique sera plus important.
• De l’autre côté, l’investissement dans l’éducation pousse le niveau technologique, car les gens avec plus de connaissances ont plus de probabilité d’inventer et innover.

Époque Malthusienne

Cette période représente la plus longue durée du modèle et comprend le temps entre l’apparition des êtres humains modernes (homo sapiens) il y a environ 100 000 ans jusqu’à debout du 18è siècle. L’époque Malthusienne se caractérise par le nul effet des développements technologiques sur le revenu par tête. C’est-à-dire, les améliorations technologiques permettant de produir davantage n’ont aucun effet sur le niveau de revenu par tête. Or, pendant cette période, la production addionelle était dédiée à augmenter la fertilité: les familles avaient plus d’enfants.¹ Ainsi, pendant l’époque Malthusienne, les sociétés les plus technologiquement développées ne montraient pas un revenu par tête plus élevé mais une plus grande densité de population.

Ce type de dynamique qui génére une augmentation de la population avec chaque progrès technique peuvent se répresenter à l’aide des préférances inclouant un niveau de consommation minimale.² Ce niveau doit toujours être atteint. Or, chaque fois que la technologie s’améliore (de manière aléatoire), les revenus disponibles additionnels seront utilisés pour augmenter le nombre d’enfants. Le graphique suivant illustre la situation:

Quand le revenu par tête est faible, sans la restriction de consommation minimale (ligne verte), les familles souhaiteraient consommer peu. Mais elles sont obligées de consommer, au moins, la consommation minimale, donc l’optimum passe à être la combinaison de consommation minimale et le nombre d’enfants qui elles peuvent se permettre considérant le coût de chaque enfant: $y = c + \rho y n \implies n = \frac{y-c}{\rho y}.$ En tout moment, la technologie peut améliorer, grâce au fait que la population augmente. Ainsi, quand cela arrive, le revenu par tête augmente (la restriction budgétaire –orange– se déplace vers la droite). Or, tandis que la consommation minimale soit une contrainte contraignante, la décision optimale continue d’être: consommer le minimum et utiliser ce qui reste pour avoir des enfants. Le graphique montre ça avec les points rouges qui sont toujours sur la ligne de consommation minimale (verte) mais chaque fois plus en hauteur. Ainsi, chaque fois la population augmente plus rapidement, et cela contribue à faire avancer la technologie plus rapidement.

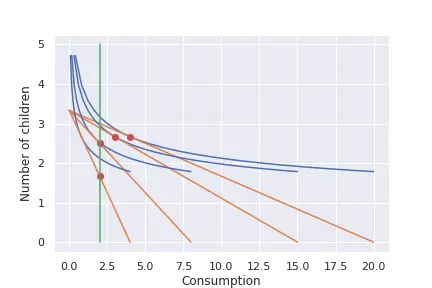
Conclusions de l’époque Malthusienne

• Corrélation positive entre:
  • Technologie et densité de population
  • Productivité agricole et densité de population
• Pas de corrélation entre:
  • Revenu par tête et technologie
  • Revenu par tête et productivité agricole
• Les pays les plus avancés du point vue technologique et les plus productives:
  • Densité de population supérieure
  • Pas de différence en revenu par tête.

Validation

Ashraf et Galor (2011) vérifient la validité des conclusions pour l’époque Malthusienne.

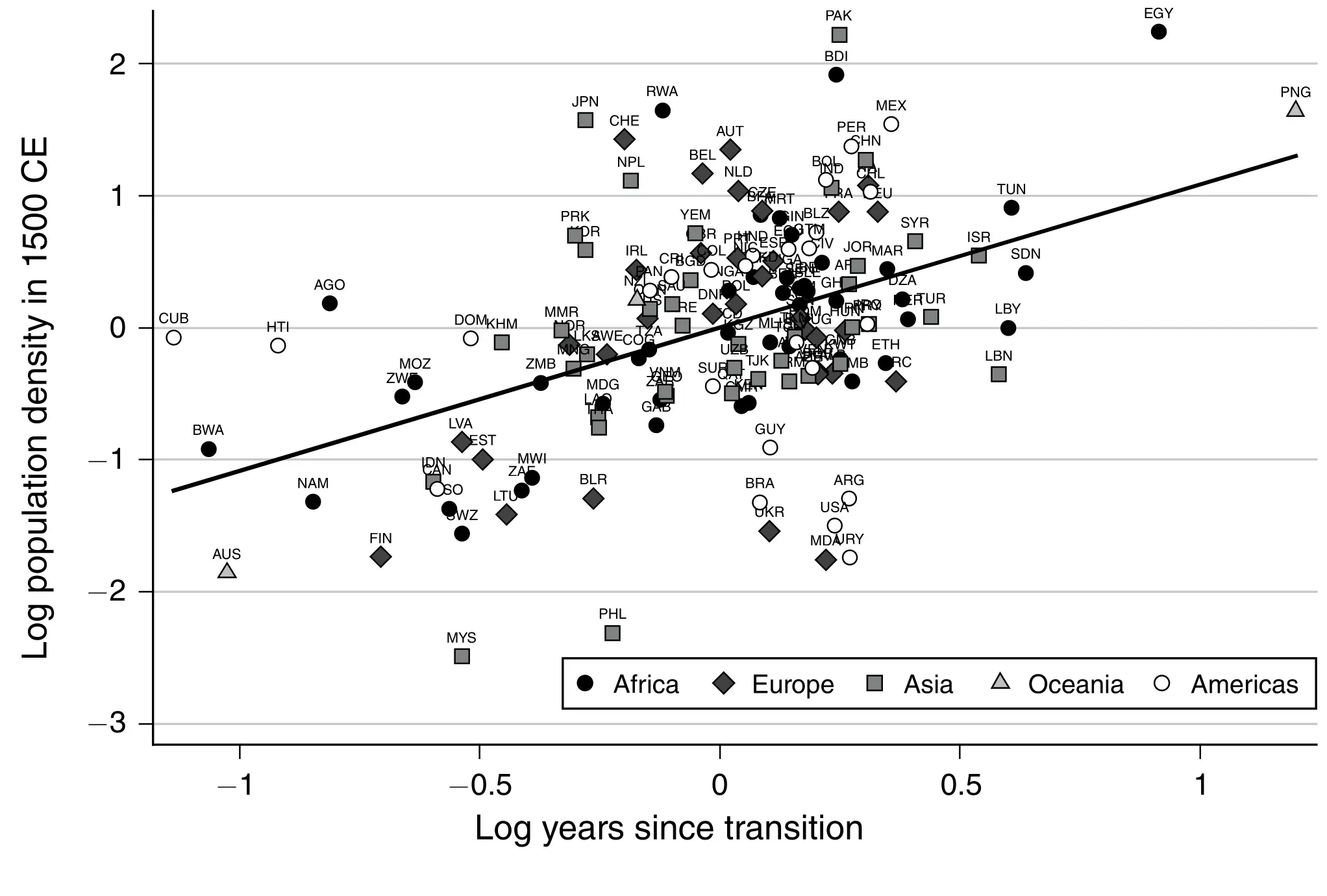
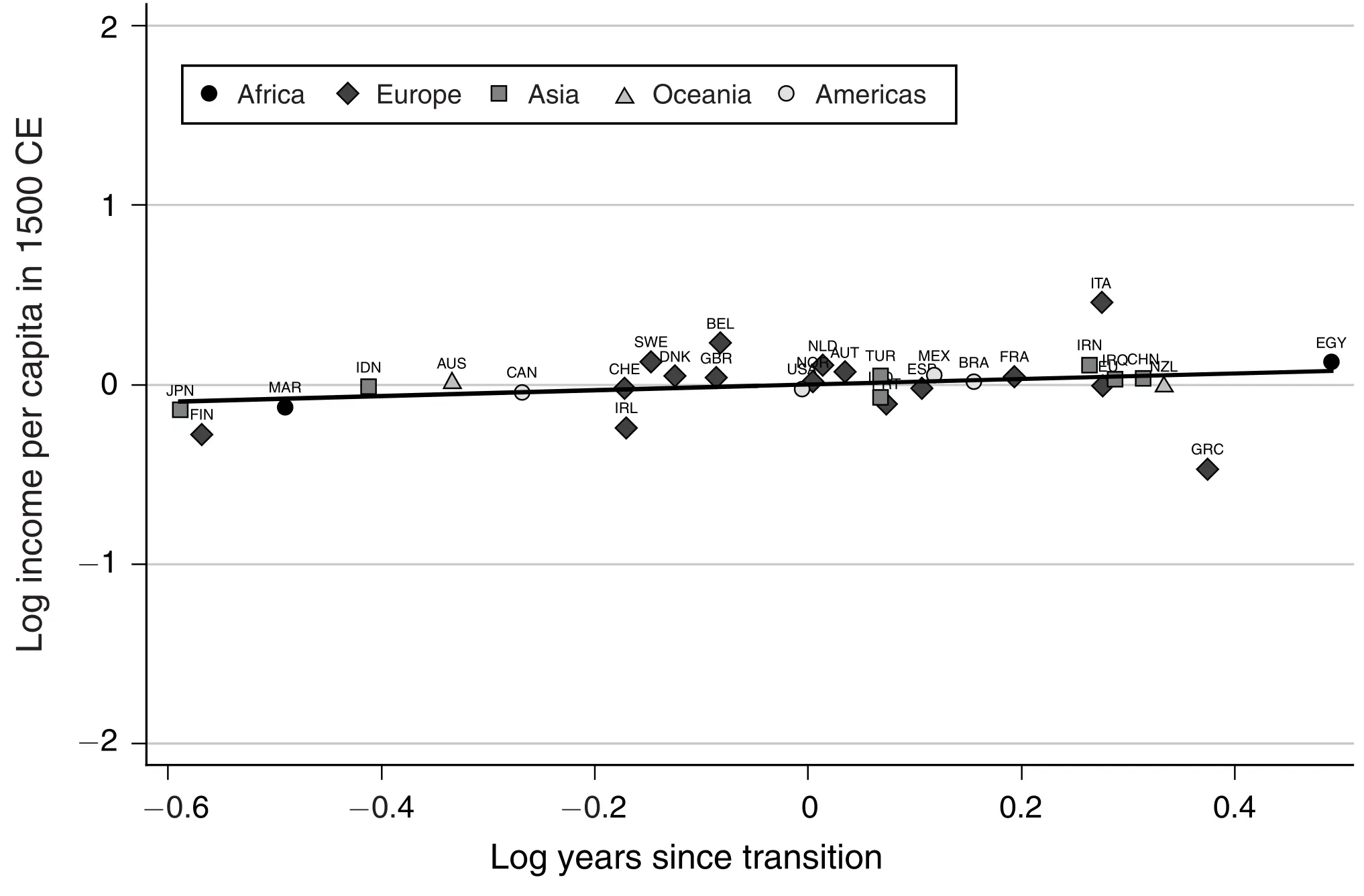
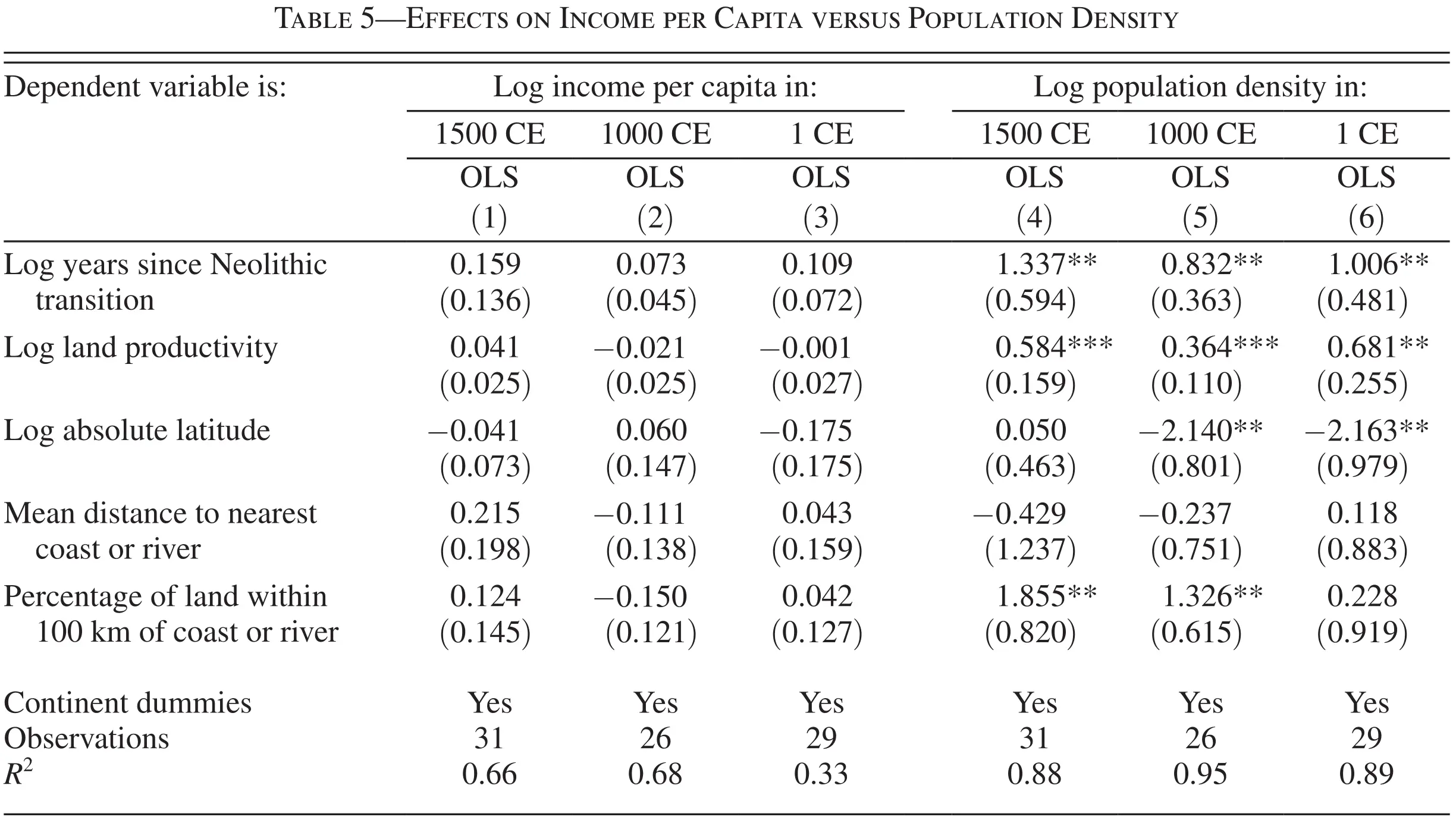
D’abord, ils montrent comment les pays qui ont du terrain plus adapté pour l’agriculture ont atteint une plus grande densité de population vers l’année 1500 mais que les gens ne jouissaient pas de plus de revenu par tête.

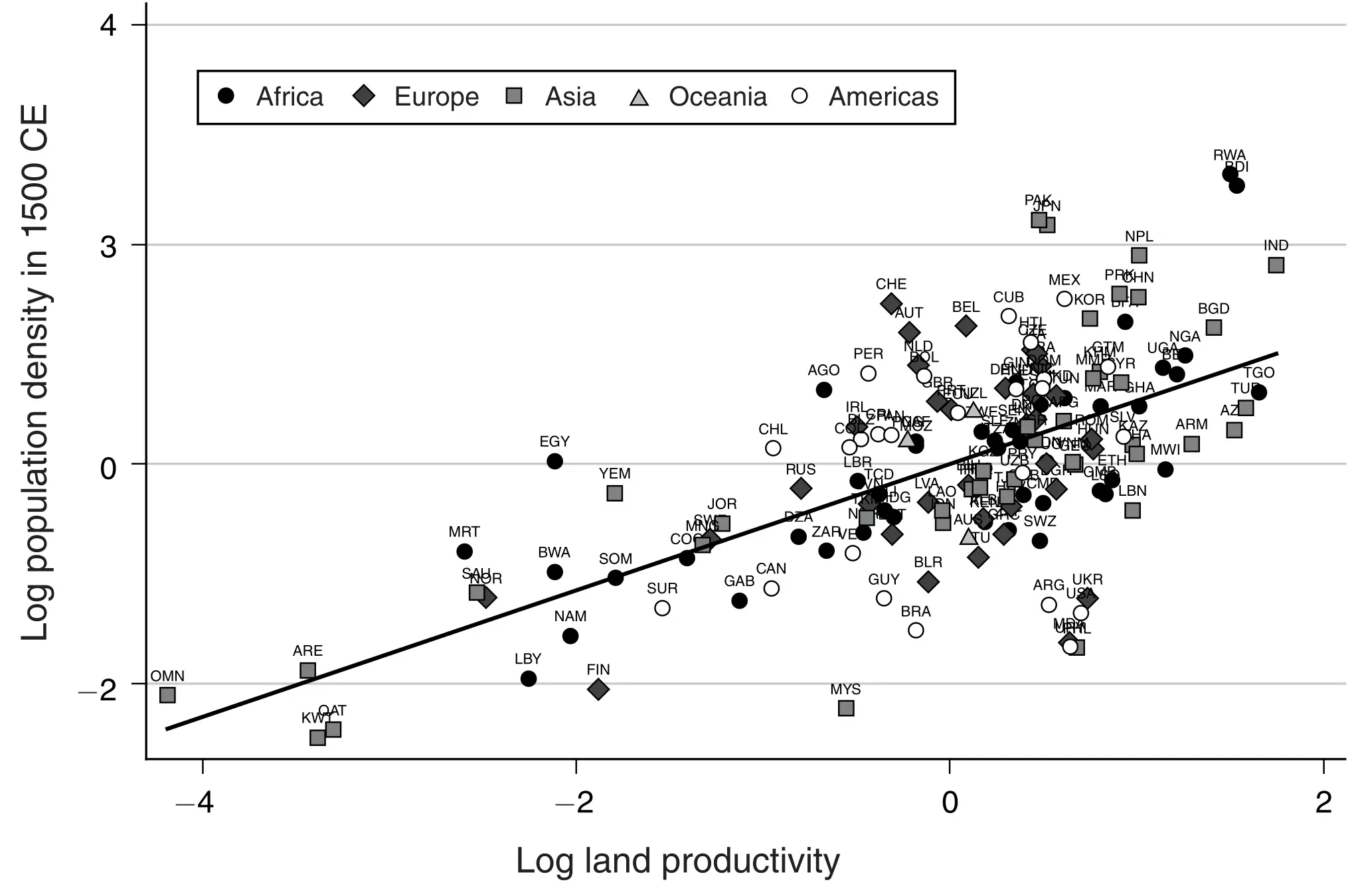
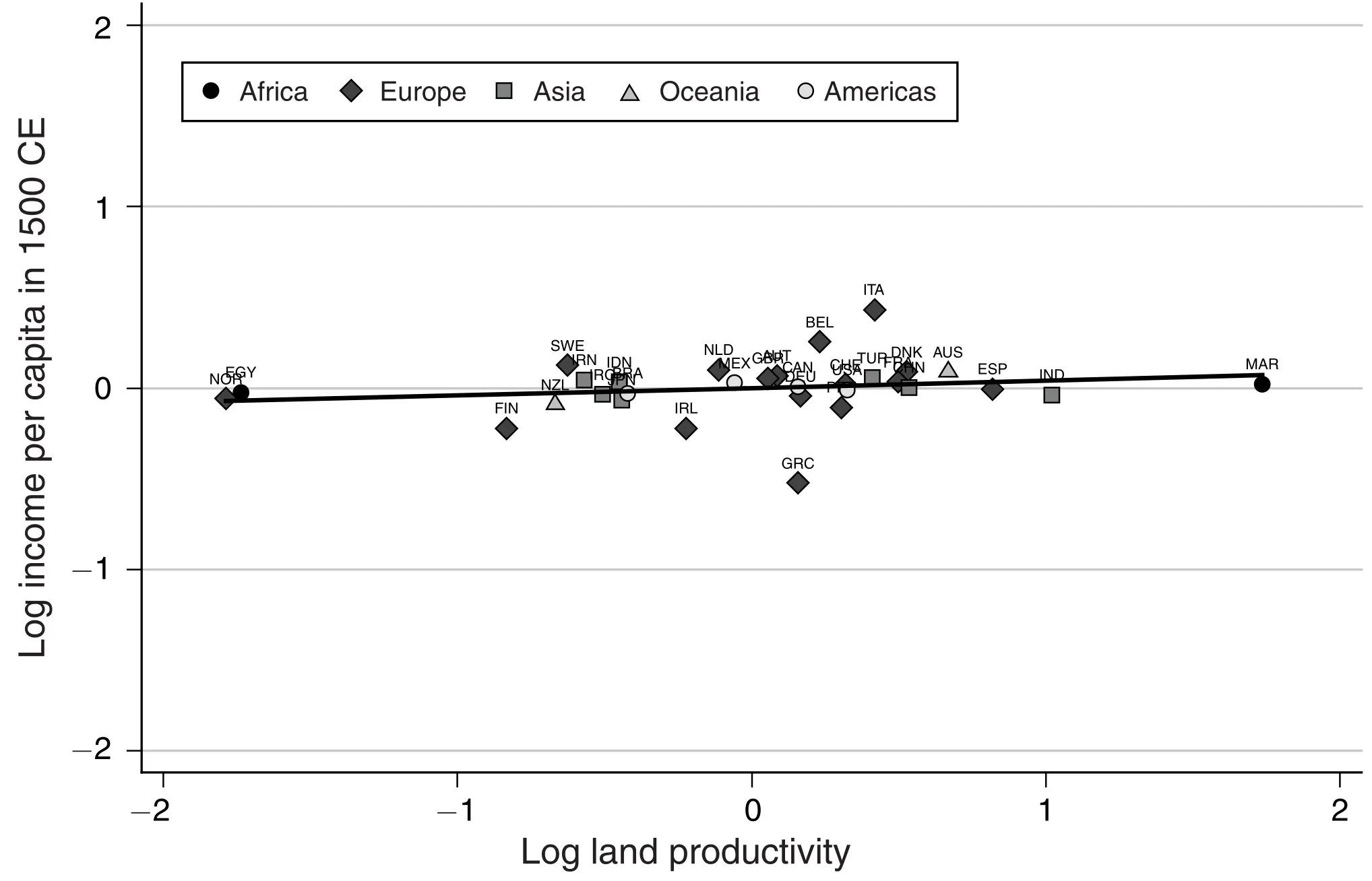
Ensuite, ils se centrent sur le lien entre technologie, densité de population et revenu par tête. L’enjeu dans ce cas est le fait que la taille de la population influence la technologie, et donc il faut être attentif du point vue économétrique. Pour résoudre le problème, Ashraf et Galor approximent le niveau technologique par le nombre d’années qui se sont passées depuis la révolution Néolithique: c’est-à-dire, les années qui se sont passées dès qu’une société adoptait l’agriculture. L’idée de base (prise de Jared Diamond (1997)) indique que les sociétés qui ont adopté l’agriculture pouvait produire d’avantage par rapport aux chasseurs cueilleurs, et donc, généraient un surplus de ressources. Ces ressources excédentaires permettaient qu’une partie de la population était dédiée à des taches non productrices de nourriture qui ont développé le langage écrit, la science, etc. En premier lieu, ils montrent que les pays et régions qui se sont passées à l’agriculture plus tôt, ont eu un avantage technologique qui se montre dans toute une série de variables qui mesurent le niveau technologique:

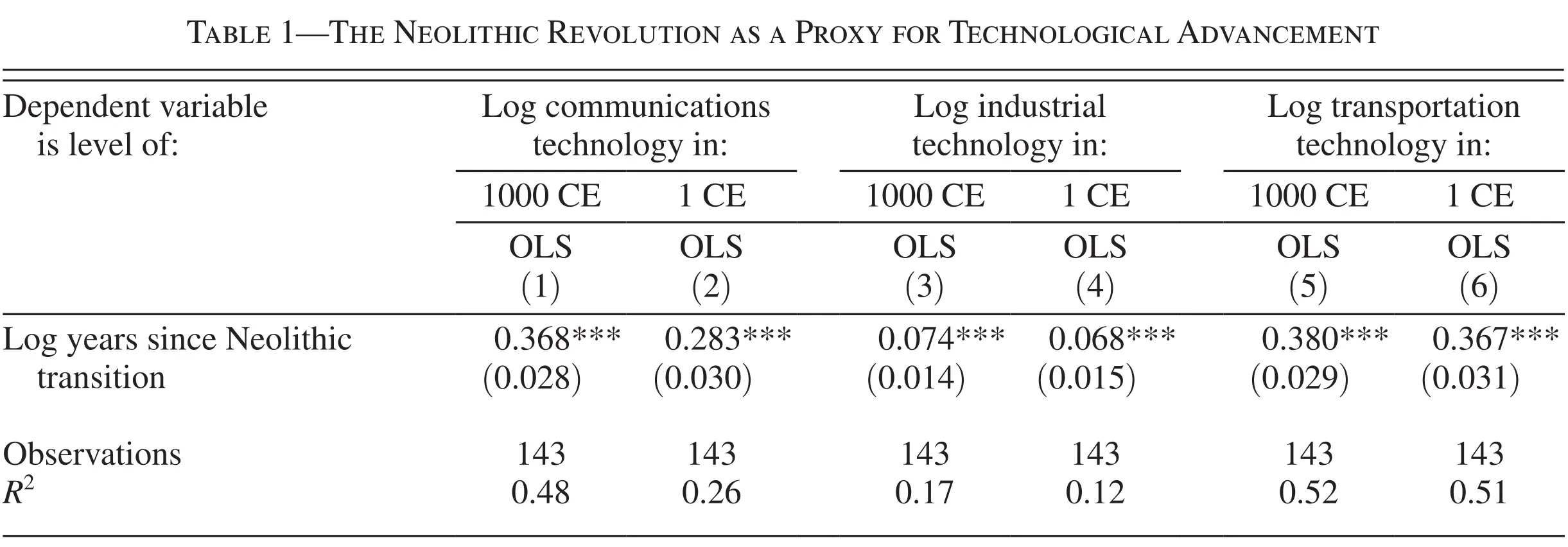
Enfin, ils montrent qu’effectivement, les pays avec plus de technologie avait plus de densité de population pendant l’année 1500 mais pas plus de revenu par tête.

Époque post-Malthusienne

Enfin, on arrive à une situation dans laquelle la contrainte de consommation minimale n’est plus contraignante: à partir de ce point-là, les familles décident d’avoir un nombre constant d’enfants et utiliser tout le revenu qui reste pour financer leur consommation. Cette deuxième période est caractérisée par le fait que la technologie avance plus rapidement grâce a l’augmentation de la population qui a eu lieu pendant l’époque Malthusienne. Par contre, le niveau de revenu par tête est encore insuffisant pour permettre les investissements en éducation. Enfin, le trait distinctif du la période post-Malthusienne est l’avancement du revenu par tête. En effet, le nombre d’enfants par parent reste constant, comme à la fin de la période Malthusienne, car les parents n’investissent encore en éducation. Par contre, comme la technologie ne cesse d’augmenter, la seule conclusion possible est que le revenu par tête doit augmenter aussi.

Pour tant, ce passage de l’époque Malthusienne à l’époque post-Malthusienne peut générer déjà différences de revenu par tête entre pays et régions. Par exemple, les pays qui, pour une raison ou une autre ont fini plus tôt leur époque Malthusienne verront leur revenu par tête augmenter, tandis que ces qui restent encore dans le système Malthusien montrent un niveau de revenu par tête qui est constant au long du temps.

Validation

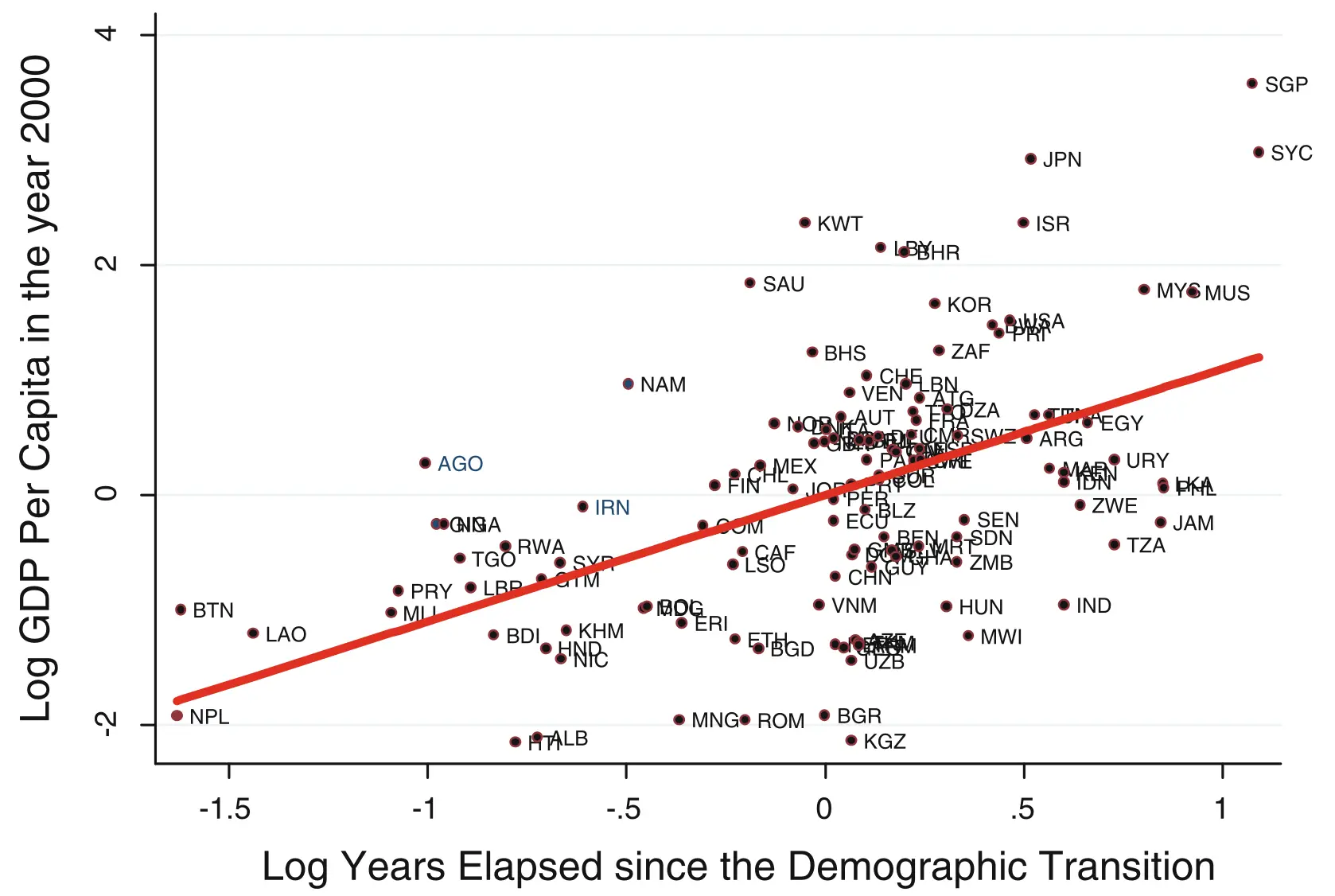
Selon la discussion au-dessous, les pays qui ont commencé leur transition démographique plus tôt, devront montrer un plus haut niveau de revenu par tête. Or, ce lien devrait exister, car il y a des avantages liés à une transition démographique précoce: le revenu par tête augmente depuis plus long temps. Galor, 2012 montre que c’est le cas:

Époque moderne

Rappelons que le niveau technologique n’a pas cessé d’augmenter pendant la période post-Malthusienne. La technologie ait tellement avancé que les parents décident qu’il est nécessaire d’investir dans l’éducation pour éviter que le capital humain de leurs enfants se déprécie. Ainsi, éventuellement, le niveau technologique atteint la valeur critique à partir de laquelle les parents sont prêts à investir en éducation. Autrement, il serait possible que le revenu par tête soit suffisamment élevé pour que les parents décident investir en éducation (selon Galor, l’évidence empirique n’est pas d’accord avec cette idée). En tout cas, la conclusion est la même: en époque moderne, les parents décident d’investir en éducation. Cela entraine un effet direct:

• Le coût de chaque enfant a augmenté, car maintenant on leur fournit de l’éducation. Pour tant, les familles décident d’avoir moins d’enfants mais de leur offrir plus d’éducation. On appelle à ce trade-off le “quality-quantity trade-off”: les familles échangent nombre d’enfants contre qualité des enfants. En plus, comme le coût des enfants est proportionnelle au revenu par tête, à mesure que celui augmente, les familles ont moins d’enfants.
  • On observe, pour tant, une corrélation négative entre revenu et nombre d’enfants.
  • On appelle à ce procès la “transition démographique”. En plus, maintenant que les enfants reçoivent éducation, la technologie augmente encore plus rapidement. En effet, la taille de la population cesse d’être la variable principale qui détermine la vitesse à laquelle la technologie avance, et l’éducation prend le relai. Enfin, la combinaison d’une population qui augmente plus lentement et une technologie qui s’améliore plus rapidement implique que le revenu par tête augmente de manière soutenue.

Conclusions de l’époque moderne

• Corrélation positive entre:
  • Revenu par tête et dépense en éducation
• Corrélation négative entre:
  • Revenu par tête et fertilité

La théorie unifiée de la croissance économique unifié et les inégalités économiques

La théorie unifiée de la croissance économique propose un nouveau paradigme de croissance économique qui comprend l’entérite de l’histoire humaine. De manière résumée, les facteurs principaux derrière la croissance économique sont l’évolution de la technologie et la demande de capital humain. Ainsi, on peut penser que tout facteur qui donne un avantage en relation à ces deux éléments, est capable de générer des différences économiques entre régions. Voici quelques exemples que nous allons voir en cours:

• Géographie:
  • Conditions bio-géographiques conduisant à la révolution Néolithique (Diamond, 1997)
  • Maladies, espérance de vie et investissement en capital humain (Andersen, Dalgaard et Selaya, 2012)
  • Culture conduisant à l’innovation (Özak, 2018)
• Caractéristiques transmisses intergénérationalement:
  • Préférence vers le présent et le futur (Galor et Özak, 2016)
  • Diversité (Ashraf et Galor, 2013)
• Colonialisme:
  • Frontières artificielles (Papaioannou et Michalopoulos, 2012)
  • Esclavage (Nunn, 2008)