Optimality

Note: Based on de la Croix and Michel, Chapter 2 and Gorth’s lecture notes.

The first welfare theorem states that a competitive equilibrium is Pareto optimal. However, the first welfare theorem has two requisites the Diamond model does not meet: a finite number of goods and a finite number of agents. Therefore, the allocation resulting from the competitive equilibrium may not be Pareto optimal.

The golden-rule level of capital

We begin the discussion by bringing back the idea of over- and under-accumulation of capital we have seen before. In the Diamond model —and different from the Ramsey model—, the capital stock on the balanced growth path may exceed the golden-rule level. This implies that a permanent increase in consumption is possible.

When discussing the golden-rule level of capital, we are not interested in how consumption is divided between the old and the young. Rather, we seek to maximise total consumption during one period. In fact, if we maximise total consumption, the ensuing allocations between young and old will be efficient. First, let $\mathfrak{C}_t$ represent total consumption: $$\mathfrak{C}_t \equiv C_t + D_t.$$ The economy-wide resource constraint dictates that total production is either consumed or invested:

$$\mathfrak{C}_t + K_{t+1} = F(K_t, N_t)+ (1-\delta)K_t.$$

Alternatively, aggregate consumption per unit of labour is:

$$\mathfrak{c}_t \equiv \frac{\mathfrak{C}_t}{N_t} = \frac{F(K_t, N_t) +(1-\delta)K_t - K_{t+1}}{N_t} = $$ $$ = f(k_t) + (1-\delta)k_t - (1+n)k_{t+1}.$$

The golden-rule level of the capital-labour ratio $k^\mathcal{GR}$ is the value of the capital-labour ratio $k$ that results in the highest possible sustainable level of consumption per unit of labour. The fact that it is sustainable requires that it is replicable forever. For this reason, we consider the steady state with $k_{t+1} = k_t = \bar{k}$. The resource constraint at the steady state simplifies to:

$$\bar{\mathfrak{c}} = f(\bar{k})-(\delta + n)\bar{k} \equiv \mathfrak{c}(k).$$

We maximise this function with respect to $\bar{k}$:

$$\mathfrak{c}^\prime(\bar{k}) = f^\prime (\bar{k}) - (n+\delta) = 0$$ The fact that $\mathfrak{c}^{\prime \prime}(\bar{k}) = f^{\prime \prime}(\bar{k})<0$ assures that we have the maximum.

Assuming that $n+\delta >0$ and that $f$ satisfies:

$$\lim_{k \rightarrow +\infty} f^\prime(k) < n+ \delta < \lim_{k \rightarrow 0} f^\prime(k),$$

then $\mathfrak{c}^\prime(\bar{k}) = f^\prime (\bar{k}) - (n+\delta) = 0$ has a solution in $\bar{k}$ and it is unique. Hence, the golden-rule level of capital is given by:

$$f^\prime(k^\mathcal{GR}) = n + \delta.$$

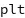
The highest sustainable consumption level per unit of labour is obtained when, at steady state, the net marginal productivity of capital equals the growth rate of the economy.

Over- and under-accumulation of capital

The golden-rule level of capital is given by $f^\prime(k) = n+\delta.$ However, in the decentralised economy, the steady-state level of savings is highly unlikely to coincide with it. For instance, a log-utility function coupled with a Cobb-Douglas production function leads to a steady-state value of capital such that $f^\prime (k) = \frac{\beta}{(1+n)(1+\beta)}^\frac{1}{1-\alpha}.$ In general, $\frac{\beta}{(1+n)(1+\beta)}^\frac{1}{1-\alpha} \neq n+\delta.$

If the steady-state level of the economy is such that $f^\prime (\bar{k}) < n+ \delta,$ the economy has accumulated too much capital: if $f^\prime (\bar{k}) < f^\prime(k^\mathcal{GR}) \implies \bar{k} > k^\mathcal{GR}.$ Conversely, if the interest rate at the competitive steady state is such that $f^\prime (\bar{k}) > n + \delta,$ then it lacks capital compared to the golden rule.

Improving the situation: dynamic inefficiency

Let’s suppose for the moment that the decentralised economy reaches a situation of over-accumulation of capital, this is, $f^\prime(\bar{k}) < n + \delta.$ It is possible to improve upon it by means of redistribution. Simply, a planner could order young individuals to save less, as to reach $k^\mathcal{GR}.$ Doing so increases the available total output per worker, which can be consumed either by the old or the young, improving their utility. In subsequent periods, the economy would remain at $k^\mathcal{GR}$, which maximises total output per worker.

In particular, assume we impose a lump-sum tax on all young individuals and we transfer it to the old generation. The transfer is fully consumed (old individuals gain utility from consuming it). Suppose the transfer is one good from each young to the old. There are $1+n$ young individuals per old individual, so the old receive $1+n$ goods. Let’s repeat this scheme every period.

• The young transfer one good to the old
• Consumption of the young does not change because they refrain from saving.
• In the future, they receive $1+n$, which represents a return rate of $1+n$ on their “investment”.
• In the competitive market, they would have obtained $f^\prime(k) < n + \delta.$
• Clearly, the return young individuals achieve under the tax system is larger, and hence they are better off.

At the same time, old individuals are also better off. In the first period, when the reform is introduced, they consume more. Later generations obtain a higher return for the tax they pay, leaving them better off, too.

When organising such scheme is possible, we say that the competitive economy was dynamically inefficient.

Note: it is possible to solve the dynamic inefficiency introducing money. Young individuals would exchange goods for paper notes with the expectation of exchanging them back again when old.

Dynamic efficiency

In the opposite case, when $\bar{k} < k^\mathrm{GR}$, reaching the golden-rule level of capital requires increasing it. Suppose we are at time $t_0$. Increasing the capital to $k^\mathcal{GR}$ would certainly improve consumption for all generations $t > t_0$. However, young individuals at $t_0$ should forgo some consumption to save more and build the necessary capital. Hence, the consumption of the young generation at $t_0$ necessarily decreases. Our policy of improving utility for all individuals fails in this case.

We call such situations dynamically efficient: it is impossible to increase the utility of all generations.

Example

We use a log-utility and Cobb-Douglas case to illustrate over- and under-accumulation of capital.

$$U(c,d) = \log( c ) + \beta \log (d)$$ $$f(k)= Ak^\alpha.$$

The golden-rule level of capital dictates that total consumption per worker should be maximised. Using the resource constraint:

$$\max \mathcal{c_t}= f(k_t) +(1-\delta)k_t - (1+n)k_{t+1}.$$

Evaluating it at the steady state yields:

$$\max \mathfrak{c} = f(k) - (n+\delta)k \implies f^\prime(k^\mathcal{GR}) = n+\delta.$$

Hence, in our case:

$$A \alpha {k^\mathcal{GR}}^{\alpha-1} = n + \delta \implies k^\mathcal{GR} = \left(\frac{A\alpha}{n+\delta}\right)^\frac{1}{1-\alpha}.$$

In the decentralised economy, we have that:

$$k_{t+1} = \frac{1}{1+n} s(\omega(k_t), f^\prime(k_{t+1})) = \frac{1}{1+n}\frac{\beta}{1+\beta}A(1-\alpha)k_t^\alpha.$$

Hence, the steady-state level of capital is:

$$\bar{k} = \frac{A \beta (1-\alpha)}{(1+n)(1+\beta )}\bar{k}^\alpha \implies \bar{k} = \frac{A(1-\alpha) \beta}{(1+n)(1+\beta)}^\frac{1}{1-\alpha}.$$

We have capital over-accumulation if: $\bar{k} > k^\mathcal{GR} \implies \frac{(n+\delta) \beta}{(1+n)(1+\beta)} > \frac{\alpha}{1-\alpha}.$

Check Romer, pp. 89–90 for an empirical discussion about the dynamic efficiency.