Dynamiques

Dynamiques

Nous avons vu que le comportement de l’économie dans le modèle de Ramsey se décrit par deux équations dynamiques:

\begin{align} \dot{k}(t) =& w(t) + r(t)k(t) - c(t) - \delta k(t) - n k(t) \\\ \frac{\dot{c}}{c} =& \frac{1}{\sigma}(r(t) - \rho - \delta) \end{align}

La résolution de ce système d’équations permet d’obtenir l’évolution optimale du capital et de la consommation intertemporels dans le modèle de Ramsey.

Nous avons aussi les valeurs d’équilibre pour le salaire et le taux d’intérêt ($w(t),r(t)$). Pourtant, nous pouvons fermer le modèle et exprimer le système exclusivement en termes de $k(t)$ et $c(t)$. En fait:

$$\color{red}{w(t) = f(k(t)) - f^\prime (k(t)) k(t)}$$ $$\color{red}{r(t) = f^\prime (k(t))}$$

Pourtant, en équilibre, $\dot{k}(t) = w(t) + r(t)k(t) - c(t) - \delta k(t) - n k(t)$ devient :

$$\dot{k}(t) = f(k(t)) - c(t) - (n + \delta) k(t)$$

Cela a du sens: à niveau agrégé, le capital qu’on accumule est égal à tout ce qui est produit ($f(k)$) moins ce qu’on consomme ($c$) et ce qu’on perd ($\delta$). Le terme $n$ reflet l’augmentation de la population, car nous travaillons en par tête. Ainsi, le système dynamique est:

\begin{align} \dot{k}(t) =& \textcolor{red}{f(k(t))} - c(t) - (n + \delta) k(t) \\\ \frac{\dot{c}}{c} =& \frac{1}{\sigma}(\textcolor{red}{f^\prime(k(t))} - \rho - \delta) \end{align}

État stationnaire

Comme dans le modèle de Solow, on s’intéresse à l’existence d’un (ou plusieurs) état stationnaire. C’est-à-dire, une situation telle que, une fois atteinte, l’économie reste là sans plus bouger. Un état stationnaire est une situation où les variables économiques majeures comme le capital par tête et la consommation par tête restent constantes à long terme, reflétant un équilibre stable dans l’économie. Dans le modèle de Solow, il était facile de voir qu’un tel état existait car $\dot{k} = sf(k) - (n+\delta)k$ c’est une seule équation dynamique.

Dans le modèle de Ramsey, nous avons un système avec deux équations dynamiques. Cela veut dire que, dans l’état stationnaire, $k$ et $c$ doivent rester inchangés. Autrement dit, l’état stationnaire est caractérisé par: \begin{align} \dot{k} =& 0 \\\ \dot{c} =& 0 \end{align}

On indique, comme avant, les variables stationnaires avec une étoile. Ainsi, $k^\star,c^\star$ sont telles que:

\begin{align} 0 =& f(k^\star) - c^\star - (n + \delta) k^\star \\\ 0 =& \frac{1}{\sigma}(f^\prime(k^\star) - \rho - \delta) \end{align}

Il est possible de montrer qu’un tel état doit exister et qu’il a $k^\star > 0,c^\star>0$.¹

Pour analyser la stationnarité des deux variables $k$ et $c$ de manière indépendante, on commence par étudier les conditions des variables pour lesquelles $\dot{c}= 0$ et $\dot{k} = 0.$

c-locus

Tout d’abord, débutons l’analyse en étudiant les dynamiques de la consommation dans le modèle de Ramsey. L’équation $\frac{\dot{c}}{c} = \frac{1}{\sigma}(f^\prime(k) - \rho - \delta)$ montre comment $c$ évolue en fonction de $k$ (car $k$ est la seule variable qui apparaît). Premièrement, intéressons-nous aux valeurs de $k$ pour lesquelles la consommation ne change pas. Cela nous permet d’obtenir une partie de l’état stationnaire, car il comprend à la fois $k$ et $c$. Si la consommation reste constante, alors $\dot{c} = 0$ et par conséquent: $$0 = \frac{1}{\sigma}\left(f^\prime(k) - \rho - \delta\right).$$ $$0 = \left(f^\prime(k) - \rho - \delta\right).$$ $$k = f^{{\prime}^{-1}}(\rho + \delta)$$

La dernière ligne indique la valeur spécifique de $k$ pour laquelle $c$ ne change pas, Cependant, nous pouvons également démontrer de manière simple que lorsque $k$ prend une valeur différente de cette valeur d’équilibre, la consommation $c$ change. Procédons à cette démonstration !

La fonction $f^\prime(k)$ est décroissante, avec $\lim_{k\rightarrow 0}f^\prime(k) = \infty$ et $\lim_{k\rightarrow +\infty} f^\prime(k) = 0.$ Puisque $\rho + \delta > 0$, il doit exister une valeur entre $(0, +\infty)$ telle que $f^\prime(k) = \rho + \delta.$ Ceci est une application du Théorème des valeurs intermédiaires Par exemple, si $f(k)$ est une fonction Cobb-Douglas, soit $f^\prime(k) = \alpha k^{\alpha-1}$, alors la valeur $k$ pour laquelle $\dot{c} = 0$ est $k = \left(\frac{\rho+\delta}{\alpha}\right)^{\frac{1}{\alpha-1}}.$ Visuellement:

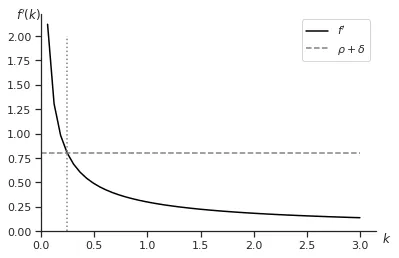
Pour simplifier, dissons que quand $k = k^\spadesuit \implies \dot{c} = 0.$ Nous avons identifié que lorsque $k=k^\spadesuit$m cela implique que $\dot{c} = 0.$ Examinons maintenant ce qui se passe lorsque $k$ prend une valeur différente, par exemple $k > k^\spadesuit.$ Pour ce faire, nous utilisons l’équation dynamique de $c:$ $$\frac{\dot{c}}{c} = \frac{1}{\sigma}(f^\prime(k) - \rho - \delta).$$

Lorsque $k > k^\spadesuit$, cela implique que $f^\prime(k) \lt f^\prime(k^\spadesuit)$, car la fonction $f^\prime(k)$ est décroissante. En revenant à notre équation dynamique de $c:$ $$\frac{\dot{c}}{c} = \frac{1}{\sigma}(f^\prime(k) - \rho - \delta) \lt \frac{1}{\sigma}(f^\prime(k^\spadesuit) - \rho - \delta) = 0.$$

Nous observons que lorsque $k \gt k^\spadesuit$, l’équation dynamique de $c$ est négative, ce qui signifie que $\dot{c} \lt 0$ et que la consommation diminue. Graphiquement:

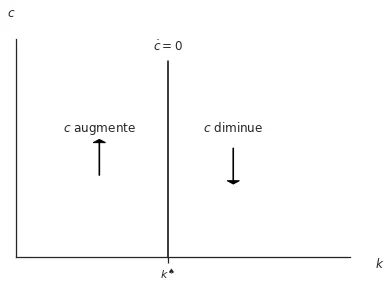
k-locus

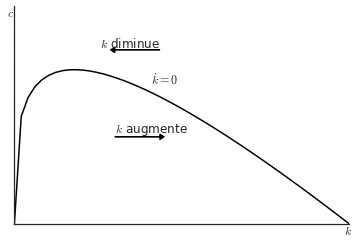
Nous procédons de manière similaire pour le capital. Dans ce cas-là, nous cherchons les combinaisons de $k$ et $c$ pour lesquelles le capital reste inchangé. Ceci est clair en observant l’équation dynamique du capital: $\dot{k} = f(k) - c - (n+\delta)k.$ Ainsi, si $\dot{k} = 0$, alors $$c = f(k) - (n+\delta)k$$ le capital ne change pas.

Avec une fonction Cobb-Douglas, le capital reste constant si $c = k^\alpha - (n+\delta)k.$ Il est clair qu’il s’agit des combinaisons de capital et consommation. Par exemple, si $\alpha = 0.3, n = 0.1, \delta = 0.1$, quand $k = 1$ et $c = 1^{0.3} - (0.1 + 0.1)\times 1 = 0.8$ le capital ne change pas. Nous pouvons le vérifier car $\dot{k} = 1^{0.3} - 0.8 - (0.1 + 0.1)\times 1 = 0.$ En revanche, si $c = 0.5$, alors $\dot{k} = 1^{0.3} - 0.5 - (0.1 + 0.1)\times 1 = 0.3 > 0$ et le capital augmente.

Nous pouvons tracer toutes les combinaisons de $k$ et $c$ qui impliquent $\dot{k} = 0.$ Étant donné les propriétés de $f(k)$ et le fait que $\dot{k} = 0 \implies c = f(k) - (n+\delta)k$, la courbe aura la forme d’une parabole inversée. De manière graphique:

État stationnaire et diagramme de phase

L’état stationnaire de l’économie est défini comme la combinaison de $k$ et $c$ telle que $\dot{k} = \dot{c} = 0.$ Ainsi, puisque nous avons deux courbes, une pour $\dot{k}= 0$ et une autre pour $\dot{c} = 0,$, l’état stationnaire correspond au point où ces deux courbes se croisent.

Enfin, nous pouvons combiner les dynamiques de $k$ et $c$ pour trouver les dynamiques de l’économie grâce à un diagramme de phase. La combinaison divise l’espace en quatre quadrants, avec des dynamiques distinctes dans chaque quadrant.

• Bas-gauche: $k$ augmente, $c$ augmente
• Haut-gauche: $k$ diminue, $c$ augmente
• Bas-droite: $k$ augmente, $c$ diminue
• Haut-droite: $k$ diminue, $c$ diminue

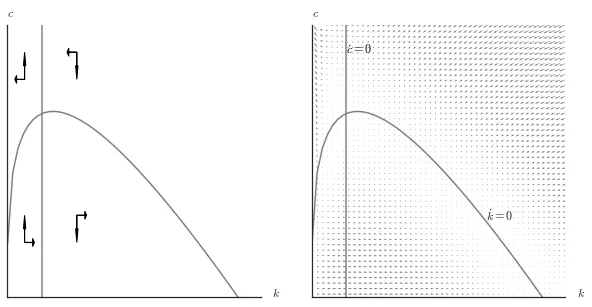
Dans le modèle de Ramsey, la plupart de trajectoires sont indésirables, car l’économie finit avec:

• Soit pas de capital ($k = 0$) et, par conséquent, pas de production ni de consommation
• Soit pas de consommation ($c = 0$).

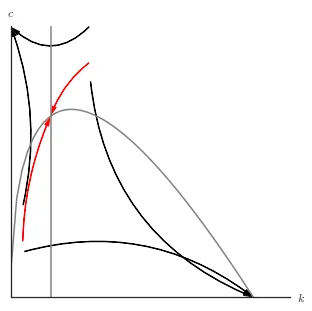
Néanmoins, il existe deux chemins (saddle path) qui mènent vers le point stationnaire.² Note: dans le modèle de Ramsey, le niveau de consommation stationnaire est inférieur au maximum qu’il pourrait atteindre. Cela est dû au fait que les ménages sont impatients et préfèrent consommer aujourd’hui.