L'état stationnaire dans le modèle de Solow

L’état stationnaire

On définit l’état (ou les états) stationnaires d’un modèle dynamique comme une configuration des variables dans laquelle les variables deviennent constantes une fois cette configuration est atteinte. Voir aussi l’Appendice.

Le modèle de Solow a une seule équation dynamique : celle du capital par habitant¹. Cette équation montre comment le niveau de capital par habitant change avec le temps :

$$\dot{k} = s f(k) - (n+\delta)k = s k^\alpha - (n+\delta)k$$

Par exemple, avec $s=0.5$, $\alpha=0.3$, $n=0.1$ et $\delta=0.1$, lorsque le niveau de capital est de $k=2$, on trouve $\dot{k} = 0.21$. Cela signifie que le niveau de capital par habitant augmente de 0.21. Ainsi, à la période suivante, le capital est de 2.21 et il augmentera de 0.19.

Comme la pente de la courbe $f(k)$ et $sf(k)$ diminue lorsque $k$ augmente, à mesure que le capital par habitant s’accumule, la vitesse d’accumulation se réduit. Cela est dû au fait que $f^{\prime \prime}(k) = \alpha (\alpha-1)k^{\alpha-2} < 0$.

En même temps, chaque unité de capital par habitant subit un processus de dépréciation qui est constant. Par conséquent, si $n+\delta = 0.2$, par exemple, avec 2 unités de capital, la dépréciation est de 0.4, et avec 2.21 unités, elle est de 0.442.

Imaginons une économie qui commence avec peu de capital ($k(0) \approx 0$). À ce niveau, la productivité du capital est très élevée (pente de la courbe $f(k)$). En même temps, avec peu de capital, la dépréciation est négligeable. Par conséquent, $\dot{k} > 0$ et le capital s’accumule. Maintenant, le niveau de capital a augmenté, la productivité diminue et le coût de dépréciation augmente. Ainsi, la deuxième augmentation du capital est plus faible. Ce processus se poursuit et aboutit à un point où le capital cesse d’augmenter : l’état stationnaire.

Mathématiquement, si l’état stationnaire est le point où les variables du modèle ne changent plus, cela signifie que l’état stationnaire est caractérisé par $\dot{k} = 0$. Cela correspond à :

$$\dot{k} = 0 \implies sf(k) = (n+\delta)k \implies s k^\alpha = (n+\delta)k$$

Ainsi, le niveau de capital qui correspond à l’état stationnaire est donné par :

$$k^\star = \left(\frac{s}{n+\delta}\right)^{\frac{1}{1-\alpha}},\text{ou},k^\star=0$$

Exactement, une fois que l’économie atteint le niveau de capital $k^\star$, le capital cesse de changer et l’économie se stabilise à cet état stationnaire. Pour le vérifier, nous pouvons calculer le taux de variation du capital $\dot{k}$ lorsque $k=\left(\frac{s}{n+\delta}\right)^\frac{1}{1-\alpha}$.

Par exemple, avec $s=0.5$, $\alpha=0.3$, $n=0.1$ et $\delta=0.1$, le niveau stationnaire du capital est $k^\star = 3.7$. En vérifiant l’équation $\dot{k}\big{|}_{k=3.7} = 0.5 \times 3.7^{0.3} - (0.1+0.1) \times 3.7 = 0$, nous constatons que le taux de variation du capital $\dot{k}$ est nul à ce niveau stationnaire. Il est simple de vérifier que si $k=0$, l’éparge est 0 et aussi la dépréciation.

Diagramme de phase

Nous pouvons illustrer la situation à l’aide d’un diagramme de phase qui montre $\dot{k}$ en fonction de $k$.

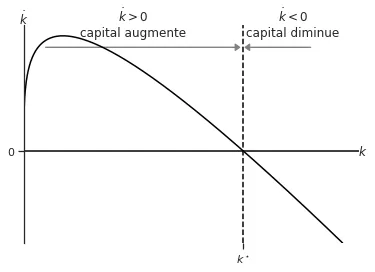
Dans ce diagramme, nous représentons directement la valeur de $\dot{k}$ pour chaque valeur de $k$. Si $\dot{k} > 0$, cela signifie que l’économie accumule du capital, tandis que si $\dot{k} < 0$, cela indique une perte de capital. La perte de capital résulte du fait que l’épargne n’est pas suffisante pour compenser la dépréciation.

Nous pouvons également observer que lorsque $k$ est éloigné de $k^\star$ (l’état stationnaire), $\dot{k}$ est élevé, ce qui signifie que l’économie accumule du capital à un rythme rapide. À mesure que nous nous approchons de $k^\star$, cette vitesse d’accumulation diminue.

Changement du taux d’épargne

Dans le modèle de Solow, les différentes politiques mises en œuvre par les gouvernements sont plus susceptibles de modifier la valeur du taux d’épargne. Par exemple, pendant la période de la COVID, les ménages allemands ont épargné beaucoup plus que d’habitude. Il est naturel de se demander comment l’économie évolue suite à ce changement de paramètre².

Imaginons que l’économie se trouve à son état stationnaire et que le taux d’épargne $s$ augmente. Cela signifie qu’un nouvel état stationnaire apparaît : $k^\star_{\text{new}} = \left(\frac{s_{\text{new}}}{n+\delta}\right)^\frac{1}{1-\alpha}$. Dans le graphique suivant, l’économie passe de la situation rouge à la noire. Avec un niveau de $s$ plus élevé, elle atteint un niveau stationnaire plus important.

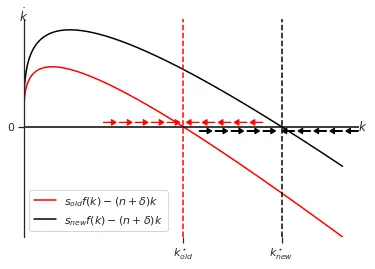
Par contre, la transition vers le nouvel état stationnaire n’est pas immédiate. Au moment où l’épargne change, l’économie se trouve avec un niveau de capital initial $k_{t=0}$, et ce niveau de capital ne peut changer qu’avec le cycle épargne-investissement. Cependant, lorsque le taux d’épargne passe de $s_{\text{old}}$ à $s_{\text{new}}$, le niveau de capital se trouve à gauche du nouvel état stationnaire. Cela signifie que l’économie suit des changements dynamiques :

1. Rappel : à l’état stationnaire, l’épargne compense exactement la dépréciation, et le niveau de capital $k$ reste inchangé.
2. Lorsqu’il y a une augmentation de l’épargne, l’économie commence à accumuler du capital, car maintenant ce qui est ajouté à l’économie est supérieur à ce qui est perdu en raison de la dépréciation.
3. Par conséquent, le niveau de capital $k$ augmente.
4. À mesure que $k$ augmente, la productivité marginale du capital diminue, ce qui signifie que chaque unité supplémentaire de capital contribue de moins en moins à la production totale.
5. En même temps, à chaque augmentation de $k$, la dépréciation augmente de manière linéaire.
6. Finalement, l’économie atteint un nouveau état stationnaire où l’épargne compense à nouveau exactement la dépréciation, et le niveau de capital $k$ se stabilise à une valeur plus élevée qu’auparavant.

Régle d’or

Le modèle Solow montre que toute économie converge vers son état stationnaire. La valeur $k^\star$ dépend du niveau d’épargne (entre autres choses) car, avec une fonction de production Cobb-Douglas : $k^\star = \left(\frac{\color{red}{s}}{n+\delta}\right)^\frac{1}{1-\alpha}$. Il est aussi clair que, avec un taux d’épargne plus élevé ($s$), le niveau stationnaire augmente. Exercice: montrez que le niveau $k^\star$ augmente avec $s$ (avec une fonction Cobb-Douglas).

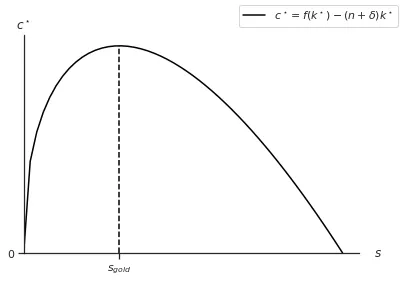
Jusqu’à présent, notre analyse a porté sur l’évolution de $k$, mais un niveau plus élevé de $k$ n’implique pas plus de bien-être. En fait, ce qui est intéressant à regarder est le niveau de consommation. Rappelons que la consommation est la partie non épargnée : $c = (1-s)f(k)$. Imaginons que l’économie se trouve à l’état stationnaire, ainsi $c^\star = (1-s)f(k^\star)$. Avec un taux $s$ faible, on consomme une grande partie de la production (terme $1-s$), mais on ne produit pas beaucoup car $k^\star$ est petit (terme $f(k^\star)$). Et inversement, avec un taux d’épargne élevé, on produit beaucoup mais on consomme une fraction petite. Y a-t-il un niveau d’épargne optimal qui maximise la consommation à l’état stationnaire ?

La réponse est oui : la règle d’or ($s_{\text{gold}}$). À l’état stationnaire, $c^\star = (1-s)f(k^\star) = f(k^\star) - \color{red}{sf(k^\star)}$. La définition d’état stationnaire est $\dot{k} = sf(k^\star) - (n+\delta)k^\star = 0$. Par conséquent, à l’état stationnaire, nous avons que $\color{red}{sf(k^\star) = (n+\delta)k^\star}$, et nous pouvons remplacer cette expression dans l’équation de consommation. Ainsi, nous avons :

$$c^\star (s) = f(k^\star) - (n+\delta)k^\star.$$ Avec la fonction de production Cobb-Douglas, nous avons :

$$c^\star (s) = {k^\star}^\alpha - (n+\delta)k^\star = \left(\frac{s}{n+\delta}\right)^\frac{\alpha}{1-\alpha} - (n+\delta)\left(\frac{s}{n+\delta}\right)^\frac{1}{1-\alpha}$$ car $k^\star = \left(\frac{s}{n+\delta}\right)^\frac{1}{1-\alpha}.$

Par définition, la règle d’or est le taux d’épargne qui maximise la consommation à l’état stationnaire. Ainsi, pour le trouver, il suffit de maximiser $c^\star$ par rapport à $s$.

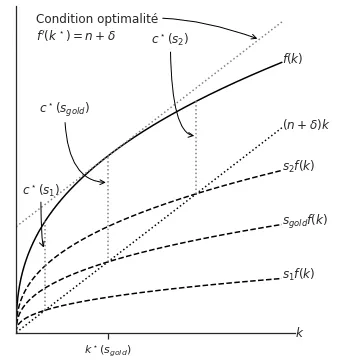
$$s_{gold} = \arg \max_{s} c^\star(s) = f[k^\star(s)] - (n+\delta)k^\star(s)$$ $$\frac{\mathrm{d} f[k^\star(s)] - (n+\delta)k^\star (s)}{\mathrm{d} s} = 0 \implies f^\prime (k_{gold}) = (n+\delta)$$

Avec la fonction de Cobb-Douglas, on peut directement observer la dépendance entre $c^\star$ et $s$ :

$$c^\star (s) = \left(\frac{s}{n+\delta}\right)^\frac{\alpha}{1-\alpha}-(n+\delta)\left(\frac{s}{n+\delta}\right)^\frac{1}{1-\alpha}$$

Si ensuite on maximise $c^\star$ par rapport à $s$ :

$$\frac{\mathrm{d} \overbrace{\left(\frac{s}{n+\delta}\right)^\frac{\alpha}{1-\alpha}-(n+\delta)\left(\frac{s}{n+\delta}\right)^\frac{1}{1-\alpha}}^{c^\star}}{\mathrm{d} s} = 0 \implies$$ $$\frac{\alpha}{1-\alpha}\left(\frac{s}{n+\delta}\right)^\frac{2\alpha-1}{1-\alpha}-(n+\delta)\frac{1}{1-\alpha}\left(\frac{s}{n+\delta}\right)^\frac{\alpha}{1-\alpha} = 0 \implies s_{gold} = \alpha$$

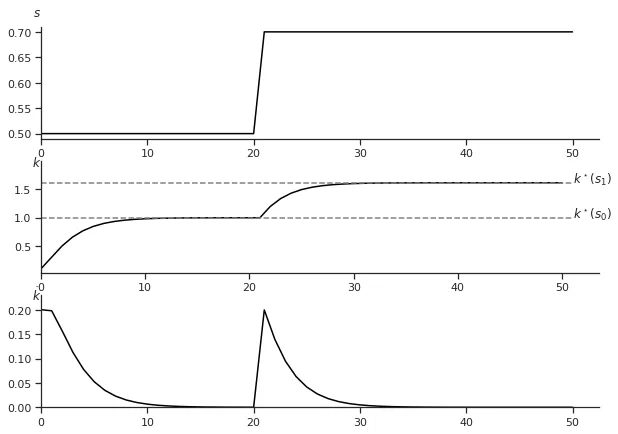
Comme nous l’avons mentionné, deux effets jouent leur rôle lorsque la valeur de $s$ change : lorsque $s$ augmente, le capital stationnaire $k^\star$ augmente, ce qui entraîne une augmentation de la production ($f(k^\star) \uparrow$).

• Comme la production a augmenté, il est possible de consommer plus ($c^\star = f(k^\star) - (n+\delta)k^\star$).
• En même temps, plus de capital implique une plus grande dépréciation ($ (n+\delta)k^\star \uparrow $).

Graphiquement, on peut observer l’effet d’un changement dans $s$ comme suit :

Inefficacité dynamique

Le taux d’épargne $s_{\text{gold}}$ est celui qui maximise le niveau de consommation à l’état stationnaire. Avec une fonction de production Cobb-Douglas, $s_{\text{gold}} = \alpha$. On peut imaginer que, pour la plupart des économies, le taux d’épargne ne coïncide pas avec l’optimal. Cependant, il est possible de déterminer les cas où l’économie pourrait faire mieux.

Imaginons que l’économie soit à son état stationnaire, et supposons que le taux d’épargne soit $s_1 > s_{\text{gold}}$. Comme $s_1 \neq s_{\text{gold}}$, la consommation stationnaire est susceptible d’être augmentée en réduisant le niveau d’épargne jusqu’à $s_{\text{gold}}$. Cela constitue une stratégie gagnante :

1. Tout d’abord, on diminue le taux d’épargne de $s_1$ à $s_{\text{gold}}$.
2. L’économie avait accumulé un niveau de capital $k^\star(s_1) > k^\star(s_{\text{gold}})$. En réduisant l’épargne, la dépréciation fait diminuer le niveau de capital, et celui-ci converge vers $k^\star(s_{\text{gold}})$.
3. Pendant la transition, le niveau de consommation est supérieur à ce qu’on avait ($c^\star(s_1)$).
4. Lorsque l’économie atteint le nouvel état stationnaire $k^\star(s_{\text{gold}})$, le niveau de consommation est maximal.

Ainsi, avec la diminution du taux d’épargne, tout le monde gagne pendant la transition et à l’état stationnaire. Ce type de situation est connu comme une situation d’inefficacité dynamique et, dans le modèle de Solow, apparaît lorsque $s > s_{\text{gold}}$.

En revanche, si $s_1 < s_{\text{gold}}$, il est impossible d’améliorer la consommation pour tous à tout moment. Il est certain que, en augmentant le niveau d’épargne, l’économie converge vers un meilleur état stationnaire. Cependant, pendant la transition, la consommation diminue : il est nécessaire d’épargner davantage, ce qui implique une réduction de la consommation.

Questions

Imaginez qu’une économie soit à son état stationnaire $k^\star$ et que $f^\prime(k^\star) > n + \delta$. Supposons qu’une politique augmente le taux d’épargne : le nouveau niveau de consommation stationnaire serait-il supérieur ou inférieur à celui d’aujourd’hui ?