Croissance économique
Croissance économique
Le modèle de Solow prédit que toute économie converge vers son état stationnaire. Ainsi, une économie qui débute avec un niveau de capital par habitant faible ($k_0$) verra celui-ci augmenter jusqu’à ce qu’il atteigne l’état stationnaire. Une fois que l’économie a atteint son état stationnaire, elle y reste. Qu’est-ce que cela signifie ?
Croissance à l’état stationnaire
Commençons par analyser l’état stationnaire. Comme $k^\star$ est constant, la production par habitant $f(k^\star)$ est également constante. Étant donné que $y^\star = f(k^\star)$ représente le PIB par habitant, la conclusion est que, à long terme, le PIB par habitant est constant. Si l’on préfère mesurer le bien-être avec la consommation par habitant, la conclusion est la même car $c^\star = (1-s)f(k^\star)$.
D’autres indicateurs, tels que le PIB total, sont également importants, et nous pouvons montrer qu’à l’état stationnaire, la consommation totale, la quantité totale de capital et le PIB total augmentent au rythme de $n$. Pour cela, il suffit de reprendre les définitions et de calculer le taux de croissance de chaque variable. On indique le taux de croissance de la variable $x$ par $g_{x}$. Lorsque le temps est continu, il se calcule comme suit: 1
$$g_{x} = \frac{\dot{x}}{x}.$$
Ainsi:
- Capital total : $k \equiv \frac{K}{L} \implies K = kL \implies g_{K} = \frac{\dot{kL}}{kL} = \frac{\dot{k}L}{kL} + \frac{k\dot{L}}{kL} = \frac{\dot{k}}{k} + \frac{\dot{L}}{L} = $ $\quad \quad g_{K} = g_{k} + g_{L} = 0 + n = n.$ Ici, $g_{k} = 0$ car nous sommes à l’état stationnaire et, par définition, $k$ est constant.
- Production totale : $y \equiv \frac{Y}{L} \implies Y = yL \implies g_{Y} = \frac{\dot{yL}}{yL} = g_{y} + g_{L} = n$ Cela est dû au fait que $y$ à l’état stationnaire est constante. Une autre manière de voir le même : $Y = K^\alpha L^{1-\alpha} \implies g_{Y} = \frac{\dot{K^\alpha L^{1-\alpha}}}{K^\alpha L^{1-\alpha}} = \frac{\alpha K^{\alpha-1}\dot{K}L^{1-\alpha} + (1-\alpha)K^\alpha L^{-\alpha}\dot{L}}{K^\alpha L^{1-\alpha}}$ $g_{Y} = \alpha \dot{K} + (1-\alpha)\dot{L} = \alpha n + (1-\alpha) n = n.$
- Consommation : $c \equiv \frac{C}{L} \implies C = cL \implies g_{C} = g_{c} + g_{L} = 0 + n.$
Croissance pendant la transition et convergence entre pays
Un pays avec un niveau de capital inférieur à son état stationnaire, c’est-à-dire $k < k^\star$, observe un processus de croissance économique vers cet état stationnaire. Pendant cette transition, le taux de variation du capital, noté $\dot{k}$, est positif et le capital s’accumule. De plus, à mesure que l’on se rapproche de l’état stationnaire, le taux de croissance du capital diminue jusqu’à atteindre zéro. Il est donc clair que pendant cette transition, on observe une croissance économique à la fois en termes de revenu par habitant et en termes de revenu total.
En effet, avec $\dot{k} > 0$, le taux de croissance du capital par habitant est positif : $g_{k} = \frac{\dot{k}}{k} > 0$. Par conséquent, la production par habitant et la consommation par habitant augmentent également. Avec une fonction de type Cobb-Douglas, nous avons: $g_{y} = g_{k^\alpha} = \alpha g_{k} > 0$ et $g_{c} = g_{(1-s)y} = g_{y} > 0$.
Les variables en termes de revenu total augmentent également plus rapidement qu’auparavant. Par exemple, le taux de croissance du capital total est donné par $g_{K} = g_{Lk} = g_{k} + g_{L} = \frac{\dot{k}}{k} + n > n$.
Convergence
Convergence absolue
Nous avons précédemment mentionné que le taux de croissance du capital par habitant est plus élevé lorsque l’économie est éloignée de son état stationnaire. En effet, le taux de croissance du capital par habitant est donné par l’équation:
$$g_{k} = \frac{\dot{k}}{k} = \frac{s f(k) - (n+\delta)k}{k} = s\frac{f(k)}{k} - (n + \delta).$$
Ainsi,
$$\frac{\partial g_{k}}{\partial k} = s \frac{\overbrace{f^\prime (k) k - f(k)}^{=(-1)w}}{k^2} \stackrel{Cobb-Douglas}{=} s (-1) \frac{\overbrace{(1-\alpha)k^\alpha}^{=w}}{k^2} < 0.$$
En conclusion, lorsque le capital par habitant s’accumule, son taux de croissance devient plus faible.
Si cela est vrai, cela signifie que les pays les plus pauvres devraient afficher un taux de croissance plus élevé. Par conséquent, nous devrions observer un rattrapage, c’est-à-dire que les pays les plus pauvres connaîtraient un taux de croissance plus élevé que les pays les plus riches, ce qui entraînerait une réduction de l’écart entre eux. Cette hypothèse selon laquelle les économies les plus pauvres ont une croissance plus forte que celle des économies les plus riches sans tenir compte de leurs caractéristiques est appelée convergence absolue. Cependant, les données rejettent clairement cette prédiction.
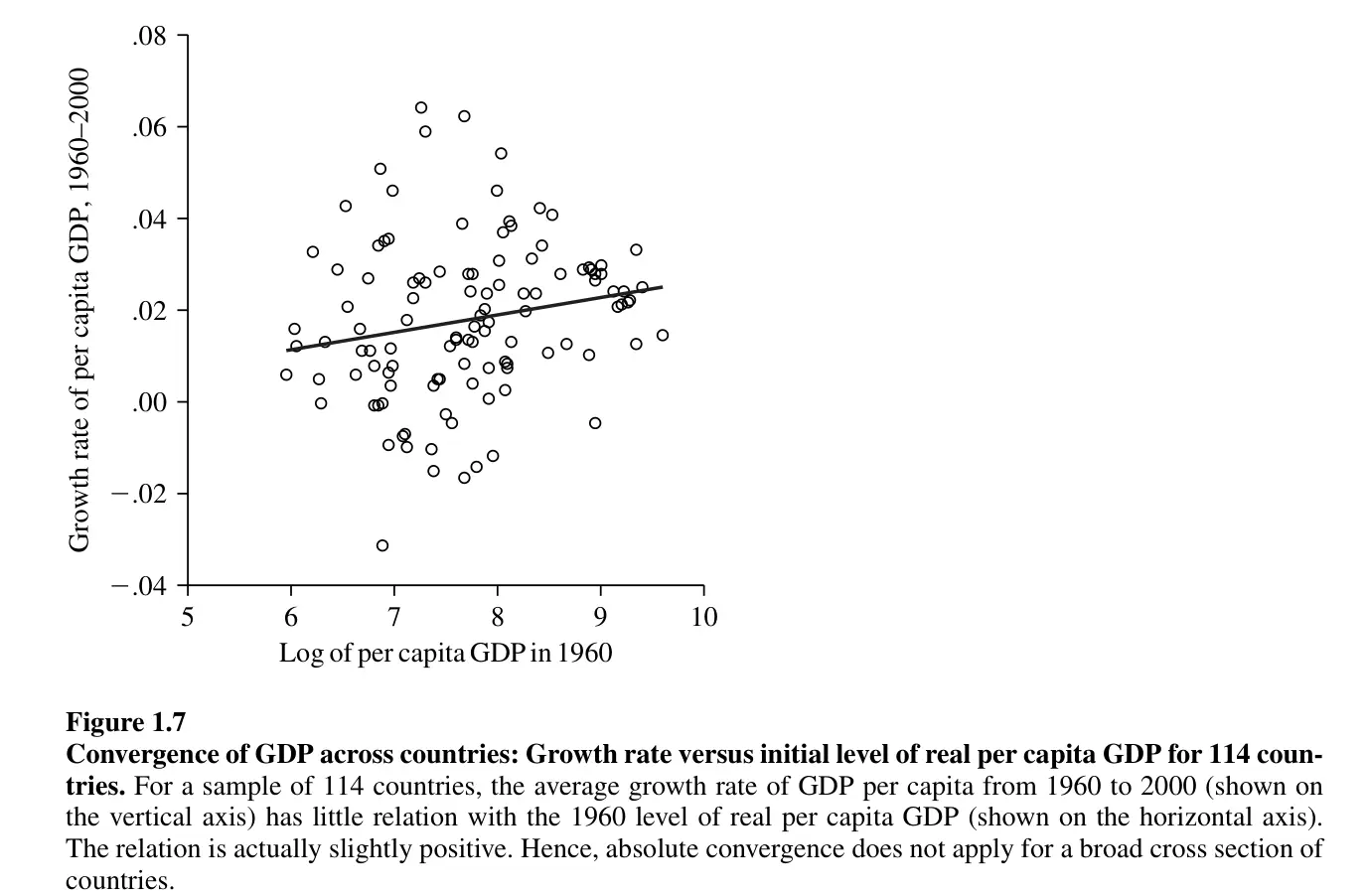
Convergence conditionelle
Une hypothèse sous-jacente à l’idée de la convergence absolue est que les paramètres de toutes les économies sont les mêmes. Dans le modèle de Solow, les paramètres du modèle incluent le taux d’épargne ($s$), le taux de croissance de la population ($n$), le taux de dépréciation ($\delta$), et la part du capital ($\alpha$). Nous avons déjà vu comment un taux d’épargne différent implique un état stationnaire différent.
S’il est vrai que des groupes de pays similaires convergent vers un même état stationnaire, alors dans ces groupes, les pays les moins riches devraient connaître un taux de croissance plus élevé que les pays les plus riches (au sein du groupe de pays). Cette idée selon laquelle des pays similaires convergent vers un même état stationnaire est appelée convergence conditionnelle, car elle dépend des caractéristiques propres aux pays. Dans ce cas, les données confirment l’idée de la convergence conditionnelle.
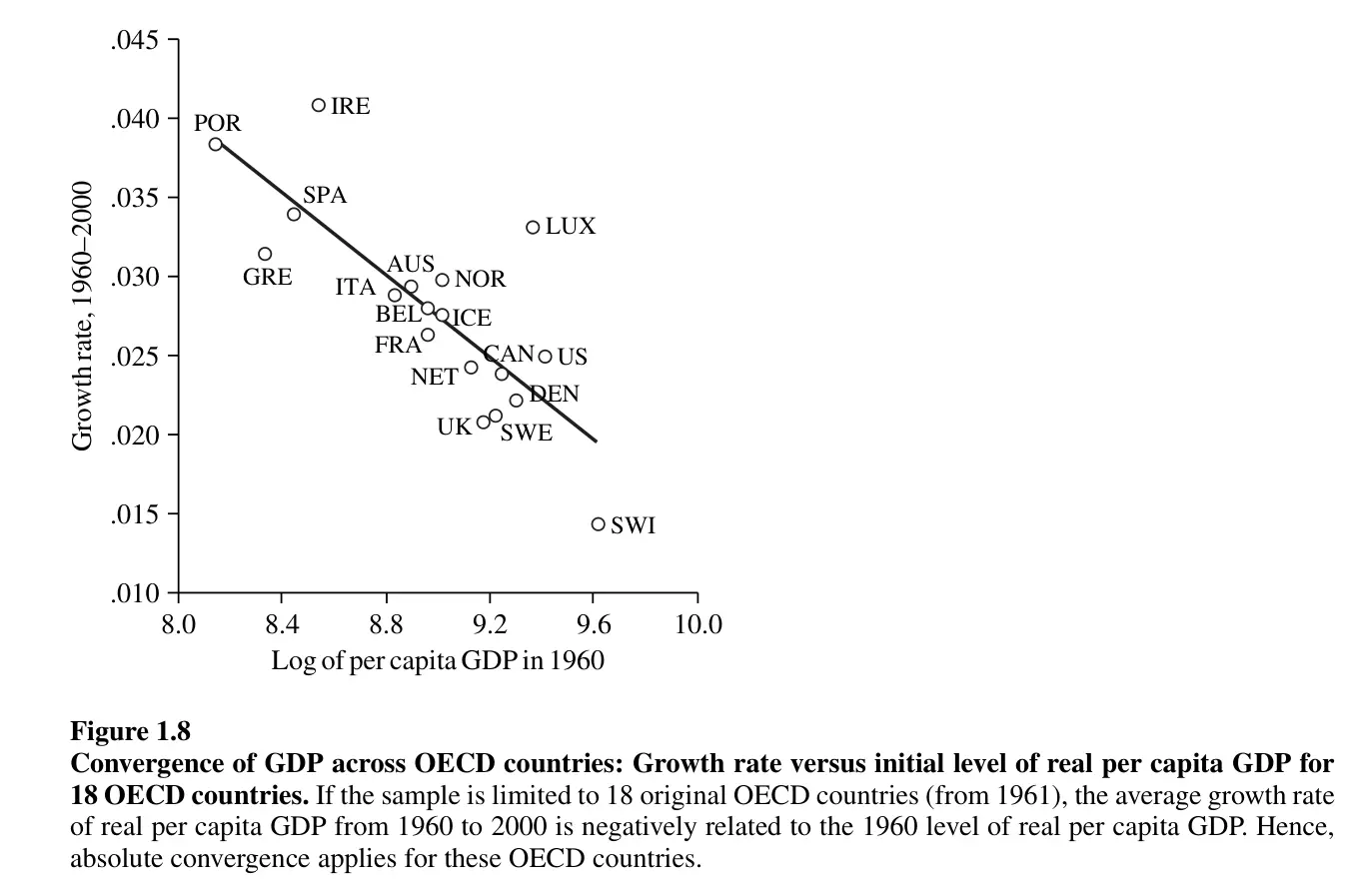
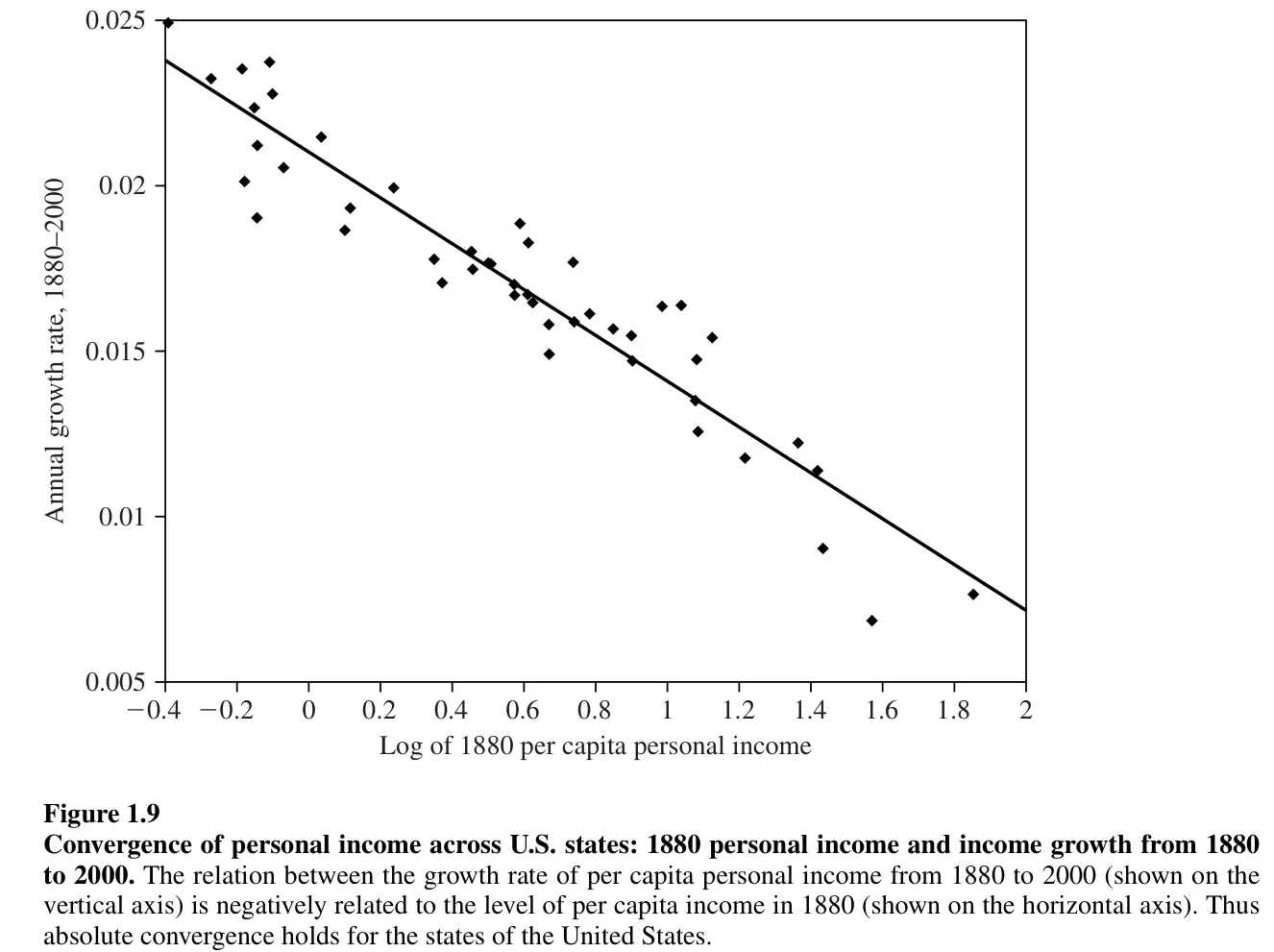
-
Quelques régles pour calculer le taux de croissance:
- $g_{XY} = g_{X} + g_{Y}$
- $g_{\frac{X}{Y}} = g_{X} - g_{Y}$
- $g_{X^\alpha} = \alpha g_{X}$