Les dynamiques dans le modèle Solow

Dérivation des dynamiques

Équation d’accumulation de capital

Le modèle de Solow repose sur une hypothèse simplifiée : le taux d’épargne est le même pour tous les ménages à tout moment. En réalité, le taux d’épargne est fixé de manière exogène dans le modèle, ce qui en fait un paramètre. Nous notons le taux d’épargne par $s$, qui représente la fraction de la production qui est épargnée¹. Il est important de noter que le taux d’épargne doit être compris entre 0 et 1, donc nous imposons $0 \leq s \leq 1.$

Comme nous l’avons mentionné précédemment, l’épargne et l’investissement sont convertis en capital productif pour la période suivante. Ainsi, l’épargne contribue à l’accumulation du capital : plus une économie épargne, plus rapidement le capital s’accumule. Cependant, cela entraîne également une réduction du niveau de consommation, car $C(t) = Y(t) - S(t) = (1-s)Y(t).$ Si le taux d’épargne est élevé, le niveau de consommation doit nécessairement être réduit.

La dépréciation du capital neutralise l’accumulation réalisée grâce à l’épargne. Nous postulons qu’à chaque période, une fraction $\delta \in (0,1)$ du capital accumulé devient obsolète et cesse d’être productif. Ainsi, si le niveau de capital est $K(t), \delta K(t)$ unités deviennent non productives.

Dérivées par rapport au temps

Nous utilisons la notation “point” pour indiquer la dérivation par rapport au temps. Cela signifie que si nous avons une fonction $x(t)$ qui dépend du temps, sa dérivée par rapport au temps est notée comme suit : $$\frac{\mathrm{d} x(t)}{\mathrm{d} t} = \dot{x}.$$

---

Tout à fait, en physique, la dérivée par rapport au temps d'une fonction qui décrit la position d'un objet donne sa vitesse instantanée à un instant donné. Par exempe, la position de l'individu est décrite par la fonction $x(t) = 2t$ où $x$ représente la position et $t$ le temps.

Pour trouver la vitesse de cette personne, nous prenons la dérivée de la fonction $x(t)$ par rapport au temps, notée $\frac{\mathrm{d}x(x)}{\mathrm{d}t}$ ou $\dot{x}$. Dans ce cas, la dérivée de $x(t)$ par rapport à $t$ est simplement 2. Donc, la vitesse de cette personne est $\dot{x} = 2.$ Cela signifie que la personne avance à une vitesse constante de 2 mètres par seconde.

---

Avec les deux hypothèses précédentes, il est possible d'écrire l'équation d'accumulation de capital pour le modèle de Solow[^1]. La _vitesse_ du capital, c'est-à-dire le _changement de son niveau_, est donnée par :

$$\dot{K}(t) = I(t) - \delta K(t) = s F\left[K(t), L(t)\right] - \delta K(t).$$

Nous pouvons penser de manière informelle à $\dot{K}(t)$ comme étant égal à $K(t+1) - K(t)$, où le $1$ dans $(t+1)$ représente une unité de temps supplémentaire, et donc on mesure le changement du niveau de capital à chaque instant.²

Comme on le voit, l’équation d’accumulation de capital dépend de la production totale : $\dot{K}(t) = s \underbrace{F\left[K(t), L(t)\right]}_{=Y(t)} - \delta K(t)$, et la production dépend du niveau de capital $K(t)$ et du nombre de travailleurs $L(t)$. Il est facile de calculer le nombre de travailleurs à un moment donné, car ils évoluent de manière exogène. Ainsi,

$$L(t) = L(0)e^{nt}.$$

De manière alternative :

$$\dot{L}(t) = \frac{\partial L(t)}{\partial t} = \frac{\partial L(0)e^{nt}}{\partial t} = n L(0)e^{nt}.$$

Ainsi, le taux de croissance de la population est :

$$\frac{\dot{L}(t)}{L(t)} = \frac{n L(0)e^{nt}}{L(0)e^{nt}} = n.$$

Accumulation de capital par habitant

Pour l’instant, l’équation d’accumulation de capital est indiquée en termes de capital total. Il serait plus pratique de l’exprimer en termes de capital par habitant, car c’est l’unité principale du modèle (on ne compare pas le PIB de la Chine avec celui du Luxembourg, on compare le PIB par habitant). Ainsi, au lieu de $\dot{K}$, nous voulons calculer $\dot{k}$. Ce changement apparemment mineur est plus complexe qu’il n’y paraît.

Attention: Nous cherchons à calculer $\dot{k} = \dot{\left(\frac{K}{L}\right)}$, où l’opérateur $\cdot$ (dérivée par rapport au temps, opérateur vitesse) est appliqué à toute la fraction $\frac{K}{L}$.

En fait, $\dot{\left(\frac{K}{L}\right)}$ est équivalent à $\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{K(t)}{L(t)}\right)$, c’est-à-dire la vitesse du capital par habitant. Cela diffère de :

• $\dot{K} \rightarrow$ vitesse du capital (sans distinction de la population)
• $\dot{K}\big{/}{L} \rightarrow$ vitesse du capital, divisée par la population
• $\frac{\dot{K}}{\dot{L}} \rightarrow$ division de la vitesse du capital par la vitesse de la population.

Comme $\dot{k} = \dot{\left(\frac{K}{L}\right)} = \frac{\mathrm{d}}{\mathrm{d} t}\left(\frac{K(t)}{L(t)}\right)$, il suffit d’appliquer les règles de dérivation¹. Ainsi :

$$\frac{\mathrm{d} \frac{K(t)}{L(t)}}{\mathrm{d} t} = \frac{ \overbrace{\dot{K}(t)}^{\frac{\mathrm{d} K(t)}{\mathrm{d} t}} L(t) - \overbrace{\dot{L}(t)}^{\frac{\mathrm{d} L(t)}{\mathrm{d} t}}K(t)}{L(t)^2} = $$ $$ = \frac{\dot{K}(t)}{L(t)} - \frac{\dot{L}(t)}{L(t)}\frac{K(t)}{L(t)} = \frac{\dot{K}(t)}{L(t)} - n k(t)$$

Ici, nous avons utilisé $\frac{\dot{L}(t)}{L(t)} = \frac{n L(0)e^{nt}}{L(0)e^{nt}} = n$ et défini $k(t) \equiv \frac{K(t)}{L(t)}$.

Cependant, nous avons encore un problème : notre expression pour $\dot{k}$ inclut $\dot{K}$, ce qui la rend peu utile. Pour la simplifier, nous utilisons $\dot{K} = s F[K,L] - \delta K$ (il est à noter que cette expression n’est pas par habitant). Ainsi, à partir de :

$$\frac{\dot{K}(t)}{L(t)} - n k(t)$$

si nous remplaçons $\dot{K}(t)$ par $\dot{K} = s F\left[K(t), L(t)\right] - \delta K(t)$, nous obtenons :

$$\frac{\dot{K}(t)}{L(t)} - n k(t) = \frac{s F\left[K(t), L(t)\right] - \delta K(t)}{L(t)} - n k(t) = $$ $$= s f(k(t)) - (n+\delta)k(t).$$

Ainsi, l’équation d’accumulation de capital par habitant est :

$$\dot{k} = s f(k) - (n + \delta) k.$$

Cette équation est l’équation fondamentale du modèle de Solow. Avec la fonction de production Cobb-Douglas, elle devient $\dot{k} = s k^\alpha - (n+\delta)k$.

Comprendre $\dot{k} = s f(k) - (n+\delta)k$

L’équation fondamentale du modèle de Solow nous indique comment le capital par habitant change avec le temps, c’est-à-dire, c’est la vitesse du capital par habitant. On y voit un facteur positif qui accélère l’accumulation de capital par habitant et un autre facteur négatif qui le freine.

• Facteur positif : $s f(k)$ Il est lié à l’épargne. En effet, si les ménages épargnent davantage ($s$ plus grand) ou si la production par unité de capital est plus élevée ($f(k)$ plus grand), alors on accumule davantage de capital. On remarque que l’épargne est une fraction de la production totale.

• Facteur négatif : $(n+\delta) k$

  On peut penser à $(n+\delta)$ comme étant le taux total de dépréciation du capital par habitant. D’un côté, si un plus grand nombre de machines deviennent inutilisables chaque année ($\delta$ élevé), alors on perd du capital. D’un autre côté, ici on parle de capital par habitant. Ainsi, si la population augmente considérablement ($n$ élevé), le nombre de machines par personne diminue ($k$ diminue).

Il est possible de représenter graphiquement les deux contributions sur un même graphique.

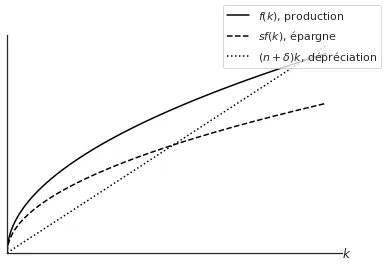
La courbe solide représente la fonction de production (intensive) : $f(k) = k^\alpha$. On peut observer qu’elle vérifie toutes nos hypothèses :

• Croissante ($f^\prime (k) > 0$)
• Concave ($f^{\prime \prime} (k) < 0$)
• Pente forte lorsque $k$ est proche de zéro ($\lim_{k \rightarrow 0} f^\prime (k) = \infty$)
• S’aplatit lorsque $k$ tend vers l’infini ($\lim_{k \rightarrow \infty} f^\prime (k) = 0$)
• La courbe commence à zéro ($f(0) = 0$)

La courbe en traits représente l’épargne-investissement. C’est, par définition dans le modèle, la fraction $s$ de la production totale, et donc elle présente les mêmes propriétés que la fonction $f(x)$.

Enfin, la droite en pointillés représente le taux de dépréciation total, incluant la “vraie” dépréciation du capital ($\delta$) ainsi que l’érosion du capital par habitant due à l’augmentation de la population $n$. La droite de dépréciation est une droite avec une pente constante égale à $n+\delta$.

Il est possible de montrer que, en raison des propriétés des courbes, un point de croisement entre $sf(k)$ et $(n+\delta)k$ existe.

Ce point de croisement est appelé état stationnaire et il constitue un élément crucial du modèle Solow et de tous les modèles dynamiques².